Apteronotus
- 201
- 0
Hi I have a question regarding the charge Q that would build up on capacitors in series when there is a potential difference between the plates.
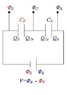
Consider the attached circuit.
1. Knowing the potentials \phi_A, \phi_B and the capacitances C_A, C_B, but not \phi_C is there a way of calculating the charges on the plates?
2. Is Q_A=Q_{Ca} and Q_B=Q_{Cb}?
3. Is Q_{Ca}=Q_{Cb}? If not, what would prevent charge flowing from one plate to the other?
4. The series capacitors are equivalent to a single capacitor having capacitance
C_T=(C_AC_B)/(C_A+C_B) and hence charge Q_T=C_TV. Is Q_A=Q_B=Q_T?
Sorry this is so long winded, and thanks in advance.
Consider the attached circuit.
1. Knowing the potentials \phi_A, \phi_B and the capacitances C_A, C_B, but not \phi_C is there a way of calculating the charges on the plates?
2. Is Q_A=Q_{Ca} and Q_B=Q_{Cb}?
3. Is Q_{Ca}=Q_{Cb}? If not, what would prevent charge flowing from one plate to the other?
4. The series capacitors are equivalent to a single capacitor having capacitance
C_T=(C_AC_B)/(C_A+C_B) and hence charge Q_T=C_TV. Is Q_A=Q_B=Q_T?
Sorry this is so long winded, and thanks in advance.