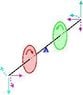
Double gyros...
Hi wysard,
Basically, let's assume the mechanical setup is ideal, that is, it is perfectly balanced with perfect frictionless bearings and infinitely rigid support and axle rod. Thus when the double gyro is rotated, even though each gyro by itself will place a perpendicular stress upon its bearings, those bearings are perfect and thus there is no vibration stimulated. The connecting axle is also infinitely rigid, and thus does not bend under stress but conveys the forces as if it were a rigid body. I also assume that there are no Special Relativity effects, such as E=mc^2 effects. In other words, when the gyros are being spun up, we add energy to them and thus according to m=E/c^2 they are slightly more massive than when the gyros are not spinning. If we neglect these effects, then I believe that since the net angular momentum is zero the gyros's axle can be moved in any direction about its central pivot point by any applied force without experiencing a 90 degree precessional motion, that is, a motion directed 90 degrees from the direction of the applied force.
In the schematic drawing, the downward applied force (solid cyan arrow) would normally result in the horizontal precession (dashed cyan arrow) if only the front (red) gyro were spinning. But with the back (green) gyro spinning in the opposite direction, the same downward force at the front would produce an upward force (darker solid cyan arrow) because of the pivot point (blue) that would normally result in the horizontal precession (darker dashed cyan arrow) if only the back (green) gyro were spinning. Assuming perfect balance and exactly opposite angular momenta, these two precessions will exactly cancel each other. The same is true for the magenta forces and their 90 degree precessions -- they too will exactly cancel in a perfect idealized setup. Notice that the cyan forces are in the vertical plane while the magenta forces are in the horizontal plane (these are thus two of the three possible directions that the axle can be pushed). The only other direction that you can push the axle is along its axis, and a force along the axis does not produce a torque since the lever arm's radius is zero (or, in other words, the cross product of the angular velocity and the pushing force is zero). Pushing along the axle thus does not produce any torque and would only produce an acceleration of the center of mass of the system (and a difference between spinning and nonspinning gyros would only be detected by an increase in mass, m=E/c^2, of the spinning gyros). Since any force applied to the axle can be decomposed into a linear combination of horizontal, vertical, and axial components, and the horizontal and vertical components produce canceling precessional motions, then, neglecting effects from Special Relativity, the double counterrotating gyros behave the same whether they are spinning or not.
As I mentioned in my first post (ever), I tried this with two lecture gyros. Now they aren't mechanically perfect, the axle isn't infinitely rigid, the bearing aren't frictionless, and it is difficult to spin them up to roughly 10K rpm and have them have exactly the same magnitudes (but opposite sign) of angular momentum. Nevertheless, I think you might be pleasantly surprised how the precessional motion vanishes when you perform the experiment. So, please have a look at the photograph of the setup - the two gyros are mounted on an axle, and the axle is suspended in a mount that allows free motion both in the vertical plane (up-down movement) as well as in the horizontal plane (rotation about a vertical axis). When one gyro is spun up, the pair behaves (obviously) just like it should if there were only one gyro --- you apply a force in one direction and the response is a precession at a 90 degree angle to the applied force (normal gyroscopic reaction, in other words). But after spinning up the second gyro in the opposite direction, then any force applied pushes the axle in the direction of the force, just as if neither gyro were spinning. When I actually perform these experiments, it is amazing how accurately the behavior of the oppositely spinning gyros repeats the behavior of the nonspinning gyros. In other words, pushing the axle with my finger behaves the same whether the gyros are not spinning or whether they are counterrotating. My only problem is getting them to spin at the same rate and thus have the same magnitudes (but opposite directions) of angular momentum. Since the spin up is accomplished by a small motor temporarily attached to the end of the gyros's axles, I have to quickly spin one up and then the other before the first one slows too much. But the gyros will spin unaided for over ten minutes on their own, so this allows me to get them fairly close in angular velocity and thus angular momentum. Any slight disparity in angular momentum (ie, slight nonzero net angular momentum) is masked by the friction in the pivot mount, thus I really do not visually observe any precession when I applying a force along any direction to the spinning double gyros.
In summary, I can push the axle of the nonspinning gyros and the unit responds by moving in the direction of my finger push. I can also push the axle of the counterrotating spinning gyros and the unit responds by moving in the direction of my finger push - same as the nonspinning case. If only one gyro is spinning and the other is not spinning, then pushing on the axle produces a motion at 90 degrees to the direction of my finger push (gyro precession, in other words). If both gyros are spinning in the same direction, then pushing on the axle produces a 90 degree motion (precession) but with a lower frequency (due to the higher angular momentum). If we allow Special Relativity effects, then the energy \Delta E = (1/2)I\omega^2 it takes to spin up the gyros makes them more massive via \Delta m=\Delta E/c^2, and this additional mass, albeit quite small, could in theory be measured.
Regards,
Syd