Capacitance (why are the charges no the same?)

[360705474]

Homework Statement

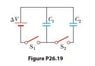
Consider the circuit shown in the attachment. Capacitor C1 is first charged by closing switch S1. Switch S1 is then opened, and the charged capacitor is connected to the uncharged capacitor by closing S2. Calculate the initial charge acquired by C1 and the final charge on each capacitor.
C1= 6.00 μF
C2= 3.00 μF
V=20.0 V

The Attempt at a Solution

This is a question from College physics book on Capacitance. I managed to solve the first subquestion. To find the final charge on each capacitor, I used Q is the same for both the capacitors after S2 is closed and S1 is open. However, the sample answer suggested that Q is different while the voltage across the capacitors are the same. I am very confused here. Because the circuit is not a close circuit (as S1 is open), I assume this situation is the same as you connect these 2 capacitors in series? Then isn't it that the charge should be the same? If not, I will be very thankful if you could help me explain it! Thank you :)

 

[cepheid]

Welcome to PF,

Actually the situation is that the two capacitors are in parallel. As a result, the voltage across them must be the same. If you think about it, suppose if the voltage across them weren't the same: then the electric fields across them would be different. This would be an unbalanced situation with a net electric field: charge would be transferred from the plates of one capacitor to the other until this net field disappeared (and the voltages were hence equal).

 

[CWatters]

Yes the voltage must be the same - apply KVL around the right hand loop when S1 made.

The total charge eg sum of charge on both capacitors at the end, will equal the charge originally on C1.

 

[360705474]

Welcome to PF,

Actually the situation is that the two capacitors are in parallel. As a result, the voltage across them must be the same. If you think about it, suppose if the voltage across them weren't the same: then the electric fields across them would be different. This would be an unbalanced situation with a net electric field: charge would be transferred from the plates of one capacitor to the other until this net field disappeared (and the voltages were hence equal).

But why the voltage is different when the capacitors are connected in series? Won't the charges move then?