Capacitor charge in parallel RC circuit

[woaname]

Homework Statement

What is Q(∞), the charge on the capacitor after the switch has been closed for a very long time?
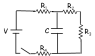
a circuit, whose image is attached, has known values for the resistors : R1 = R2 = 72 Ω, R3 = 101 Ω and R4 = 79 Ω, is C = 56 μF, V = 24 V.

Homework Equations

kirchoff's laws

The Attempt at a Solution

here is what I've calculated from preceding questions:
1) I1(0) just after the switch is closed?-------> 0.158940397 A
2) I1(∞)------------------------------------> 0.074074074 A
ive tried making the circuit at t=infinity, where the capacitor will have no current. so basically it won't interfere, but i can't see how the circuit changes?

 

[BruceW]

I agree with the answers you got for the previous parts. I don't understand what you mean when you say that you don't know how the circuit changes... As you said, the current through the capacitor becomes zero at t=infinity. And I'm guessing you used this fact to get the answers to the previous questions. So it looks like you do know how the circuit changes as t=infinity.

The problem you are trying to work out now is what is the charge on the capacitor at t=infinity. Well you have worked out the current through the resistors at t=infinity, so think of a way to work out the voltage across the capacitor at t=infinity. Nothing is special at t=infinity, it is just handy in this problem because the current at t=infinity is fairly easy to calculate, as you have done. So don't be afraid to use the usual rules for circuit behaviour even though t is tending to infinity.

 

[CWatters]

so basically it won't interfere, but i can't see how the circuit changes?

At T->∞ the capacitor might as well not be in the circuit (because Ic=0). So take it out and work out the voltage just due to the resistors.

Then apply the well known equation that relates the charge on a capacitor to it's voltage.

 

[woaname]

yes BruceW, it just took a little doodling and experimenting, but i figured out the question. thanks for your input :D, and CWatters, thanks to you too

 

[BruceW]

no problem :) glad to help.