SUMMARY
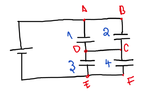
The discussion centers on the configuration of capacitors in a circuit, specifically whether capacitors 1 and 2 are in parallel and capacitors 3 and 4 are also in parallel, leading to a series connection between the two groups. The correct interpretation is that capacitors 1 and 2 are indeed in parallel, as are capacitors 3 and 4, resulting in the overall configuration being (1 P 2) S (3 P 4). Misunderstandings arise when assuming that capacitors 1 and 3 or 2 and 4 are in series without a direct connection ensuring equal potential between nodes. The flaw in the original reasoning is clarified by emphasizing that series components must carry the same current, which is not the case here.
PREREQUISITES
- Understanding of capacitor configurations: series and parallel
- Familiarity with circuit theory concepts, including node potential
- Knowledge of equivalent capacitance calculations
- Ability to interpret circuit diagrams accurately
NEXT STEPS
- Study the principles of series and parallel capacitor combinations
- Learn how to calculate equivalent capacitance for complex circuits
- Explore circuit simplification techniques, including node reduction
- Review electrical circuit analysis methods to ensure accurate interpretations
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in analyzing or designing capacitor networks will benefit from this discussion.