- #1
Hannah7h
- 40
- 0
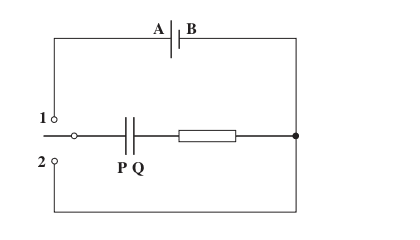
So, is this true for when a capacitor charges through a fixed resistor (as shown in the image below, when the switch is closed to 1)- the potential difference across the resistor exponentially decreases to zero and the potential difference across the capacitor exponentially increases from zero to equal the voltage across the battery (power supply), when the capacitor is fully charged?