Carnot Theorem: Understand Terms & Impossibility of Heat Engines

[Kushwoho44]

Hi there, I hold an engineering degree and I was just reviewing a page on Wikipedia.

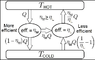
This image specifically demonstrates the impossibility of two theoretical heat engines having different efficiencies between two heat reservoirs. The full Wikipedia page can be found: https://en.wikipedia.org/wiki/Carnot's_theorem_(thermodynamics)

The terms in green I could arrive at and they confirm my understanding.

The terms in red have confused me. If I can get one of the terms, I can necessarily deduce the other and then it becomes clear to me why this cycle is impossible.

However, without knowing either of these terms, I can't understand how they have arrived at one of them alone. I suspect that they have deduced the η_m/η_l Q term from the definition of efficiency. Herein is the knot in my understanding. Why would a definition of efficiency not include a total ratio of all the energy entering the heat pump and all the energy leaving the system? I cannot understand why the definition of efficiency does not include the energy coming into the system from the cold reservoir?

Kind regards.

 

[Andrew Mason]

The Wikipedia article assumes that both systems are reversible. A heat engine has an efficiency of W_out/Q_h = (Q_h-Q_c)/Q_h = 1 - Q_c/Q_h. In reverse, applying the work output of the heat engine (stored in a spring, say) to the same system operated in reverse (as a heat pump), the heat flows are the same but in reverse direction.

The system on the right is being driven in reverse using the work output of the heat engine on the left. Since the work output of a heat pump is always negative (work must be done ON it), if you apply the concept of heat engine efficiency to a heat pump, the efficiency is always negative: ie. Work output/Heat flow in. But that is not what the author of the diagram is doing. For the system on the the author is using Work input/Heat flow to hot reservoir as the "efficiency" of the right system, which gives the same result as efficiency for that system operating in the forward direction as a heat engine .

The author supposes that the system on the right is reversible but less efficient than the one on the left, which means that when the right system is operated in reverse, using the work output of the left engine to run the right system in reverse, the heat flow to the system from the cold reservoir is a bit greater in magnitude than heat flow to the cold reservoir in the left system. This means that the heat flow to the hot reservoir is similarly greater in magnitude than the heat flow from the hot reservoir in the system on the left. As a result, there is net heat flow from cold to hot which violates the second law. So the conclusion is that no reversible heat engine operating between two reservoirs can have an efficiency lower than any other reversible engine operating between those same reservoirs. So all such reversible engines must have the same efficiency - one that is determined only by the temperatures of the reservoirs.

AM

 

[Kushwoho44]

The Wikipedia article assumes that both systems are reversible. A heat engine has an efficiency of W_out/Q_h = (Q_h-Q_c)/Q_h = 1 - Q_c/Q_h. In reverse, applying the work output of the heat engine (stored in a spring, say) to the same system operated in reverse (as a heat pump), the heat flows are the same but in reverse direction.

The system on the right is being driven in reverse using the work output of the heat engine on the left. Since the work output of a heat pump is always negative (work must be done ON it), if you apply the concept of heat engine efficiency to a heat pump, the efficiency is always negative: ie. Work output/Heat flow in. But that is not what the author of the diagram is doing. For the system on the the author is using Work input/Heat flow to hot reservoir as the "efficiency" of the right system, which gives the same result as efficiency for that system operating in the forward direction as a heat engine .

The author supposes that the system on the right is reversible but less efficient than the one on the left, which means that when the right system is operated in reverse, using the work output of the left engine to run the right system in reverse, the heat flow to the system from the cold reservoir is a bit greater in magnitude than heat flow to the cold reservoir in the left system. This means that the heat flow to the hot reservoir is similarly greater in magnitude than the heat flow from the hot reservoir in the system on the left. As a result, there is net heat flow from cold to hot which violates the second law. So the conclusion is that no reversible heat engine operating between two reservoirs can have an efficiency lower than any other reversible engine operating between those same reservoirs. So all such reversible engines must have the same efficiency - one that is determined only by the temperatures of the reservoirs.

AM

Thank you - I have now fully grasped this concept with aid of your explanation.

The principle missing cog for me was : In reverse, applying the work output of the heat engine (stored in a spring, say) to the same system operated in reverse (as a heat pump), the heat flows are the same but in reverse direction.