subbby
- 22
- 0
Attachments
Description
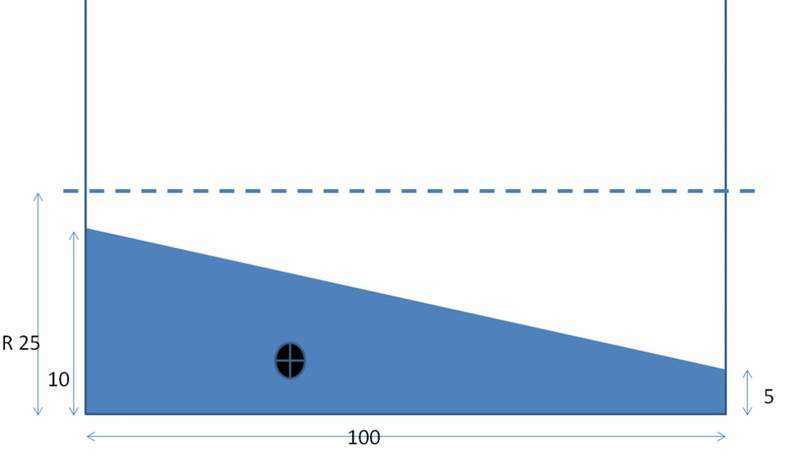
The blue is the mass inside a cylinder. In steady condition, I would want to know where its Center of gravity point shall be from either of the ends. Technically its like one mentioned in figure # 2 .It can be regarded as a portion of cylinder
Trials :
1) Divided them as a rectangle and a triangle and tried to combine the CG . (answer did not match with 3D models)
Workout :
Combined Center of gravity = area of Rectangle*Center of gravity of Rectangle + Area of triangle* Center of gravity of triangle/(Area of Rectangle+ Area of Triangle)
In this case, (taking all from left end : CG=(500*50+250*33.33)/(500+250)
No clue why it doesn’t match with the 3D modeling software’s answers. Per software, Center of gravity = 41.89 from left Any ideas ?
- Figure # 1
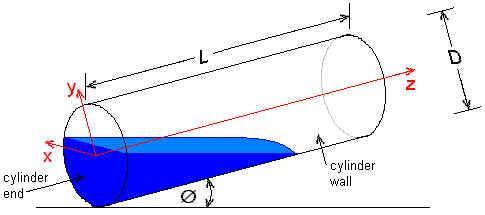
- Figure # 2 reproduced from http://www.lmnoeng.com/Volume/InclinedCyl.htmhttp://www.lmnoeng.com/Volume/InclinedCyl.htm
Description
The blue is the mass inside a cylinder. In steady condition, I would want to know where its Center of gravity point shall be from either of the ends. Technically its like one mentioned in figure # 2 .It can be regarded as a portion of cylinder
Trials :
1) Divided them as a rectangle and a triangle and tried to combine the CG . (answer did not match with 3D models)
Workout :
Combined Center of gravity = area of Rectangle*Center of gravity of Rectangle + Area of triangle* Center of gravity of triangle/(Area of Rectangle+ Area of Triangle)
In this case, (taking all from left end : CG=(500*50+250*33.33)/(500+250)
No clue why it doesn’t match with the 3D modeling software’s answers. Per software, Center of gravity = 41.89 from left Any ideas ?