Central Force with application at circle

[Arkavo]

Homework Statement

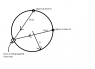
An object of mass 'm' if revolving in a circular path of radius 'R', this is analogous to a gravitational motion except that the force is applied from a point on the circle itself, it is required to find the force law

Homework Equations

from the point of application of the force..

τ=0 ⇔dL/dt=0 \Rightarrow rd\theta/dt=0 where theta is the rotation angle

The Attempt at a Solution

cant make more headway than this.. please help

 

[mfb]

What does "the force is applied from a point on the circle itself" mean?
Do you have a sketch of the setup?

Please quote the exact problem statement.

 

[Arkavo]

it means that, whereas we generally calculate the force from the center of the circle here the point if origin of the central force is on the circle itself

 

[SammyS]

What does "the force is applied from a point on the circle itself" mean?
Do you have a sketch of the setup?

Please quote the exact problem statement.

it means that, whereas we generally calculate the force from the center of the circle here the point if origin of the central force is on the circle itself

As mfb stated,

"Please quote the exact problem statement."​

 

[mfb]

A force is not "on" a circle, and if the circle itself is a physical object itself, this did not became clear.

Again: please quote the exact problem statement.

Edit: Oh, SammyS posted while I typed.

 

[Arkavo]

well this pic should show it all...

 

[mfb]

Assuming a spherical symmetry for the potential, the object has a variable velocity. Angular momentum is conserved, so you can determine the velocity everywhere (or at least the ratio of velocities). This allows to use energy conservation.

Edit: An interesting problem with an interesting solution.

 

[Arkavo]

angular momentum i can understand but how can energy be conserved i mean there is only one body in question and this is not gravitation also we have to find the force ie -dV/dr which means there's a high probability energy won't be conserved

 

[mfb]

The sum of potential and kinetic energy will be conserved, as the potential is conservative (every radial potential is conservative).

 

[Chestermiller]

I'm surprised that no one has responded to this thread during the past few days. This problem is very interesting, and I have worked out a solution, not using energy conservation, but using the kinematic and dynamic equations instead. I would like to compare notes with what other people have found. My finding was that, if the particle travels in a circular path, if the attractive body is located at the circumference of the circle, and if the line of action of the force points directly between the particle and the attractive body, then the force of attraction must be inversely proportional to the distance between the particle and the attractive body to the 5th power. I also found that the velocity and acceleration of the particle are not constant in magnitude along the circular trajectory.

But I had some issues with what is happening when the particle is in close proximity to the attractive body. I concluded that, in order for the analysis to make sense, the attractive body had to lie slightly inboard of the circular trajectory; otherwise, the particle could never accelerate along its trajectory away from the attractive body. Has anyone else obtained an inverse 5th power dependence, and has anyone else considered the issues I have mentioned when the particle is close to the attractive body?

Chet

 

[mfb]

I got the same potential.

"Close to" is not an issue (the distance is still finite). "Exactly at" is, it is not possible to consider this case in any reasonable way.