jisbon
- 475
- 30
- Homework Statement
- Two identical uniform triangular metal played held together by light rods. Caluclate the x coordinate of centre of mass of the two mass object. Give that mass per unit area of plate is 1.4g/cm square and total mass = 25.2g
- Relevant Equations
- -
Not sure what I went wrong here, anyone can help me out on this? Thanks.
EDIT: Reformatted my request.
Diagram:
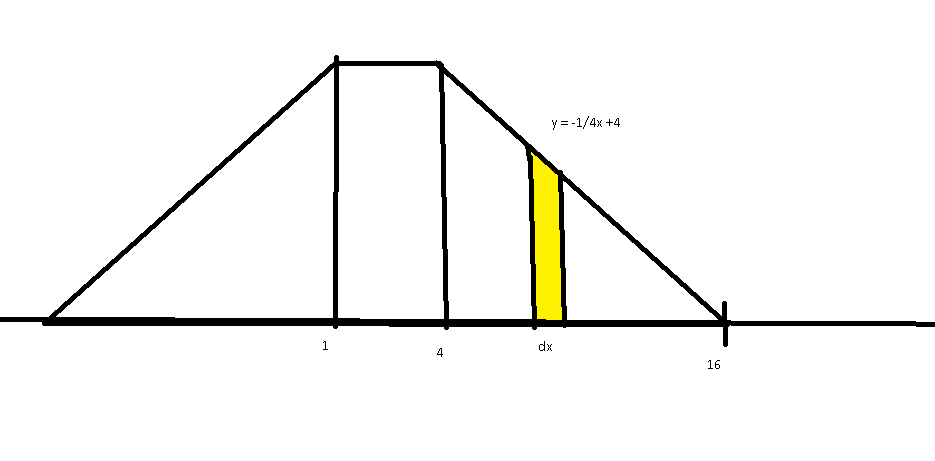
So as far as I know to calculate the center of mass for x, I have to use the following equation:
COM(x):
##\frac{1}{M}\int x dm##
And I also figured that to find center of mass, I will have to sum the mass of the 2 plates by 'cutting' them into stripes, giving me the following formula:
##dm = \mu * dx * y## where ##\mu## is the mass per unit area.
So subbing in the above equation into the first, I get:
##\frac{1}{M}\int x (\mu * dx *y) ##
##\frac{\mu}{M}\int xy dx##
Since the 2 triangles are identical, I can assume triangle on the left has equation ##y = 1/4x +4##
This is the part where I'm not sure. Do I calculate each of the triangle's center of moment, sum them and divide by 2? Or am I suppose to use another method?
Regardless of what, supposed I am correct:
COM for right triangle:
##\frac{\mu}{M}\int_{4}^{16}x(\frac{1}{4}x+4) dx## = 8 (expected)
COM for left triangle:
##\frac{\mu}{M}\int_{-11}^{1}x(-\frac{1}{4}x+4) dx## = 5.63...
Total COM = ##8+5.63/2## which is wrong :(
Thanks
EDIT: Reformatted my request.
Diagram:
So as far as I know to calculate the center of mass for x, I have to use the following equation:
COM(x):
##\frac{1}{M}\int x dm##
And I also figured that to find center of mass, I will have to sum the mass of the 2 plates by 'cutting' them into stripes, giving me the following formula:
##dm = \mu * dx * y## where ##\mu## is the mass per unit area.
So subbing in the above equation into the first, I get:
##\frac{1}{M}\int x (\mu * dx *y) ##
##\frac{\mu}{M}\int xy dx##
Since the 2 triangles are identical, I can assume triangle on the left has equation ##y = 1/4x +4##
This is the part where I'm not sure. Do I calculate each of the triangle's center of moment, sum them and divide by 2? Or am I suppose to use another method?
Regardless of what, supposed I am correct:
COM for right triangle:
##\frac{\mu}{M}\int_{4}^{16}x(\frac{1}{4}x+4) dx## = 8 (expected)
COM for left triangle:
##\frac{\mu}{M}\int_{-11}^{1}x(-\frac{1}{4}x+4) dx## = 5.63...
Total COM = ##8+5.63/2## which is wrong :(
Thanks
Last edited: