Centripetal Force/Changing direction on ice - Turn length

[testme]

Homework Statement

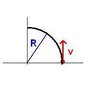
I am running to school at 6m/s when I hit a patch of icy sidealk. The coefficient of friction between the ice and my shoes is 0.16. I wish to turn my 55kg frame to the left. What is the smallest turn I can make?

v = 6 m/s
μ = 0.16
m = 55 kg

Homework Equations

Fnet = mv^2/r
Ff = μFn
Fnet = ma

The Attempt at a Solution

Assume that up and left are positive.

Fnet = ma
Fg + Fn = ma
-539 + Fn = 0
Fn = 539

Ff = μFn
Ff = 0.16 (539)
Ff = 86.24

Fnet = mv^2/r
Ff = mv^2/r
86.24 = 55(6)^2/r
86.24 = 1980/r
r = 23 m

I'm not sure if that's the answer or what to do next, or even if what I did is the right method. The question is kind of confusing me because I don't fully understand how the person is moving.

 

[ehild]

r = 23 m

I'm not sure if that's the answer or what to do next, or even if what I did is the right method. The question is kind of confusing me because I don't fully understand how the person is moving.

You got the radius of the circle (correct) the boy can turn without slipping outwards. He wants to turn to the left, change direction by 90 degrees. Instead of just turning round his body, he makes the turn along an arc. I think the problem asks the length of the arc.

ehild

 

[testme]

So you mean like a quarter of the circumference?

C = 2∏r
C = 46∏
C = 145
C/4 = 36.25m

Therefore the smallest turn the boy can make is 36.25m?

 

[ehild]

So you mean like a quarter of the circumference?

C = 2∏r
C = 46∏
C = 145
C/4 = 36.25m

Therefore the smallest turn the boy can make is 36.25m?

That is, (pi/2)*R. . Yes, I think, that was the question.

ehild