Centripetal Motion Homework: Determine Angular Velocity, Tension

[ScienceGirl90]

Homework Statement

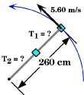
Two 4.40 kg blocks of negligible size are attached to the middle and end of a thin, massless, wire that is 260 cm long. The blocks are rotating horizontally on a frictionless horizontal surface. The free-end of the wire is attached to a pivot, and the system is rotated in such a way that the outer block is moving at 5.60 m/s.
(1)What is the angular velocity of the block attached to the middle of the wire?
(2)What is the tension T1 in the wire between the two blocks?
**picture below

Homework Equations

a_c=V_T²/r=w²r
F_c=ma_c

The Attempt at a Solution

I haven't really attempted the problem yet since I am unsure of how to start. Any help would be greatly appreciated. Thanks!

 

[tiny-tim]

I haven't really attempted the problem yet since I am unsure of how to start. Any help would be greatly appreciated.

oh come off it …

you have the equations …

apply F = ma and centripetal acceleration to each block (separately)