Chain Problem involving Kinetic Friction

[Tanya Sharma]

Homework Statement

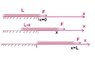
A heavy chain with a mass per unit length ρ is pulled by the constant force F along a horizontal surface consisting of a smooth section and a rough section.The chain is initially at rest on the rough surface with x=0 .If the coefficient of kinetic friction between the chain and rough surface is μ , determine the velocity of the chain when x=L .

Homework Equations

The Attempt at a Solution

I am applying work energy theorem . Work done by constant Force will be Force × displacement of centre of mass i.e FL but not able to find work done by friction .The friction force at an instant when chain length x lies on the rough surface should be μρxg.This force is continuously decreasing .i feel calculus is involved here but i am unable to apply it.Please help me .thanks.

 

[Saitama]

Work done by constant Force will be Force × displacement of centre of mass

Is the force of friction constant here?

 

[azizlwl]

It is the sum of energy taking small mass dm across the rough surface.
μgƩxdm where dm/dx=ρ
x varies from 0 to L
From this you can find the definite integral.

 

[voko]

There is not enough information. To see that, imagine the entire chain is on a smooth surface. The work of friction is zero, so the entire work must be equal to the kinetic energy at distance L. But the velocity cannot be determined because the total mass cannot be determined.

 

[Tanya Sharma]

The force of friction on chain is μN ,where N =(mass of chain on rough surface) ×g=ρxg.Thus frictional force at any instant when chain of length x is on rough surface is μρxg.But now as the chain is being pulled to right ,the length x decreases , hence frictional force decreases continually.Now i am not able to calculate the work done by this variable frictional force .What should be the limits of x when we consider dx displacement.Please reply...

 

[Tanya Sharma]

i feel sufficient information is provided.here mass per unit length ρ is provided.

 

[Saitama]

Care to check azizlwl's reply, Tanya.

 

[Tanya Sharma]

I don't understand azizlwl's reply.Kindly explain

 

[Saitama]

I don't understand azizlwl's reply.Kindly explain

You got the force of friction right. Find the work done by force of friction for small displacement dx. Integrate it from x=0 to x=L.

 

[Tanya Sharma]

why integrate from x=0 to x=L.This is the portion on smooth surface.

 

[Saitama]

Yes, it is. We have to find the work done by the force of friction when x=L i.e. L length of the chain is on the smooth surface now.

 

[Tanya Sharma]

hey Pranav...please can u give a detailed explanation.thanks. i feel limits should be between length and length - L coz intially length (full chain)was on rough surface and finally L moves to smooth surface so length - L remains on rough surface so technically we should integrate between the limits length to lenth - L.Plz help.

 

[azizlwl]

What is the total length of the chain?
I made assumption length=L.

 

[ehild]

The force acts at the right end of the chain, and the displacement of that point can be called x. x changes from zero to L, length of the chain. If the right end is at position x, L-x long piece of chain is on the rough surface. The force of friction, as you wrote correctly is proportional to the length on the rough surface. So the total force is F_t=F-μρ(L-x)g. The work of the total force is
W=\int_0^L{F_tdx}=\int_0^L{\left(F-\mu \rho g (L-x)\right)dx}.
According to the Work-Energy Theorem the work is equal to the change of kinetic energy.

ehild

 

[voko]

x changes from zero to L, length of the chain

L is not specified as the length of the chain. Nor is that apparent from the original drawing. Am I missing something?

 

[ehild]

Ops, you are right. But it seemed plausible that L is the length of the chain. Now, if it is Lc, than the work is the integral above for L≤Lc and ∫Fdx from x=Lc to L. But one does not know the mass of the chain as you pointed out, and the problem can not be solved.

ehild

 

[ehild]

There is not enough information. To see that, imagine the entire chain is on a smooth surface. The work of friction is zero, so the entire work must be equal to the kinetic energy at distance L. But the velocity cannot be determined because the total mass cannot be determined.

You are right, L should be the length of the chain...

ehild

 

[Aimless]

It seems there's some confusion amongst the previous posters on this thread, so I'm going to start from the beginning.

Two questions for Tanya:

If this problem were about a point particle of mass m, rather than a chain, would you know how to solve it?

What makes the solution for a chain different from the solution for a solid block?

My suggestion for a solution strategy for this problem is as follows. First, write down (in integral form) the equation for the change in kinetic energy of a point particle of mass m as it is pulled across both the rough and smooth portions of the table. Second, consider the chain at a given instant in time as being composed of two point particles; one on the smooth section of the surface, and one on the rough section. How does the motion of the chain affect the mass of these two imaginary point particles? Can you express that change in mass mathematically as a function of the position of the chain? If so, you should be able to write down the correct expression for the integrand of the work integral in terms of the chain's position. The last step is then to integrate.

 

[Tanya Sharma]

I am really grateful for all the prompt responses especially echild .Yes it seems that the length of chain should be L which is not mentioned in the question, but seems plausible as mentioned in above posts.Thanks a ton...