Change in rate of a man's shadow length

[Glissando]

Homework Statement

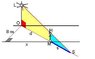
A man 1.8m tall walks at 1.5m/s along the edge of a road which is 8m wide. A street light 6.3m high is situated on the other side of the road. How fast is the length of the man's shadow changing when he is 8m past the point on the road opposite the light?

Homework Equations

Similar triangles

The Attempt at a Solution

**I'm not sure if I have the picture correct. I drew a big right triangle with one side being 6.3 and the bottom being x and y (I don't think the 8m plays a role in this question?) and I drew a smaller triangle in side and put in 1.8m.

1.8/x = 6.3/ (x+y)
1.8x + 1.8y = 6.3x
1.8y = 4.5x
1.8dy/dx = 4.5 (1.5)
dy/dx = 3.75

The answer is supposed to be 3/(5sqrt(2))

Thank you (:

 

[ehild]

Could you please show that drawing?

ehild

 

[ehild]

This is such a nice problem, I would not like to let it submerged. Here is the picture, imagine it in 3D. "s" is the length of the shadow when the man (M) has walked x=1.5 t distance from the place opposite to the lamp post L. Write s in terms of x and take the derivative with respect to time.

ehild

 

[Glissando]

Hey guys,

Thank you for the help (: I've solved it as follows:

1.8/s = 6.3/(d+s), d = sqrt(x^2+64)
6.3s = 1.8(x^2+64)^.5 + 1.8s
4.5s = 1.8(x^2 +64)^.5
4.5 ds/dt = 0.9(x^2+64)^-.5(2x)(dx/dt)
4.5 ds/dt = 0.9(8^2 + 64)^-.5(2*8) (1.5)
ds/dt = 0.4242640687 = 3/(5sqrt(2))

Thanks once again (: