ipmac
- 8
- 0
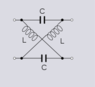
I have to find the absolute value of the transfer function for the circuit shown in the attachment. However, I have capacitors instead of inductors in my circuit and inductors instead of capacitors. So, the cross circuit will have L in the upper and lower branch and two C in the cross. I couldn't form the A-matrix of the two port circuit. Because of this the characteristic impedance couldn't be found and thus transfer function. Could you please enlighten me in this matter?