- #1
jeff1evesque
- 312
- 0
Claim:
A charged sphere will have it's charges disperse (uniformly for symmetrical objects) on the outer surface.
Proof:
Consider a sphere charged to some amount q. If we take small gaussian surfaces within the sphere, it will have [tex]\vec{E} = 0[/tex] on the closed gaussian sphere [since it is an equipotential surface]. Therefore, the electric flux is zero, so the electric charge from the small gaussian surface will have zero electric charge enclosed [Note: Gauss law states- the electric flux through any closed surface is proportional to the enclosed electric charge.
Now if we take enough small gaussian surfaces to fill the entire sphere, we find analogously the charge enclosed from all little gaussian spheres is zero. Therefore, the charge enclosed in the larger sphere is zero. But it has been charged to charge q, so the only possibility is that charge resides on the surface.
Question:
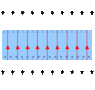
Is the proof above reasonable? Does this same reasoning apply to a single charged plate? Will charge distribute along the plate-surface where it was charged, and leave the other side uncharged [I can see why conducting spheres is a good shield in the inside, but cannot see how solid conducting plates can be used as shields respectively]?
A charged sphere will have it's charges disperse (uniformly for symmetrical objects) on the outer surface.
Proof:
Consider a sphere charged to some amount q. If we take small gaussian surfaces within the sphere, it will have [tex]\vec{E} = 0[/tex] on the closed gaussian sphere [since it is an equipotential surface]. Therefore, the electric flux is zero, so the electric charge from the small gaussian surface will have zero electric charge enclosed [Note: Gauss law states- the electric flux through any closed surface is proportional to the enclosed electric charge.
Now if we take enough small gaussian surfaces to fill the entire sphere, we find analogously the charge enclosed from all little gaussian spheres is zero. Therefore, the charge enclosed in the larger sphere is zero. But it has been charged to charge q, so the only possibility is that charge resides on the surface.
Question:
Is the proof above reasonable? Does this same reasoning apply to a single charged plate? Will charge distribute along the plate-surface where it was charged, and leave the other side uncharged [I can see why conducting spheres is a good shield in the inside, but cannot see how solid conducting plates can be used as shields respectively]?
Last edited: