Charge Distribution on Metal Sheet

[Saitama]

Homework Statement

There are two big, same size, uncharged metal sheets in the same plane, lying parallel and very close to each other. The sheets are connected through a piece of wire, and then a pointlike charge Q is placed next to them as shown in the figure. What will the amount of charge on each metal sheet be?

Homework Equations

The Attempt at a Solution

I am not sure but is this related to method of images? But I doubt so because the metal sheet is not grounded. How to proceed then?

Any help is appreciated. Thanks!

 

[BvU]

The wire equates the potential of the plates. At infinity it is 0, so so they could as well be welded together (and grounded, I guess). I think all they want from you is to integrate the induced charge in each of the two halves of the plane.

 

[Saitama]

Hi BvU! :)

The wire equates the potential of the plates. At infinity it is 0, so so they could as well be welded together (and grounded, I guess). I think all they want from you is to integrate the induced charge in each of the two halves of the plane.

Integration? Don't we simply place an image charge in method of images on the other side of conductor?

 

[BvU]

The image charge helps to find the field. So yes, that's good. You are being asked to find the charge distribution on the plates. Or rather: the integral thereof over each half-plane. Nudge nudge...

 

[Saitama]

The image charge helps to find the field. So yes, that's good. You are being asked to find the charge distribution on the plates. Or rather: the integral thereof over each half-plane. Nudge nudge...

I am not sure if I understand that. Please see the attachment. Did I place the image charge correctly? If I find the the field at point P, I can find the "local" charge density at P but how do I set up the integral?

 

[Chestermiller]

Suppose you had two identical charges of magnitude Q/2 placed symmetrically with respect to the centerline. What would the charges on the two plates be? Suppose you had two charges of magnitude -Q/2 and +Q/2 placed symmetrically. What would the charges on the two plates be?

Chet

 

[Saitama]

Hi Chestermiller! :)

Suppose you had two identical charges of magnitude Q/2 placed symmetrically with respect to the centerline.

I have indicated the centerline, do you mean that?

Suppose you had two charges of magnitude -Q/2 and +Q/2 placed symmetrically. What would the charges on the two plates be?

Do I have to place an image charge for -Q/2 and Q/2?

 

[Chestermiller]

Hi Chestermiller! :)I have indicated the centerline, do you mean that?

yes.

Do I have to place an image charge for -Q/2 and Q/2?

The figure has them reversed from the way I intended.

chet

 

[Saitama]

Sorry for the delay in reply.

The figure has them reversed from the way I intended.

chet

I have fixed the sketch but I still don't know how to proceed with the problem. Do I place the image charges as shown in the sketch?

 

[Chestermiller]

Sorry for the delay in reply.


I have fixed the sketch but I still don't know how to proceed with the problem. Do I place the image charges as shown in the sketch?

No. Get rid of the ones below the plate. Just leave the ones above the plate. Now, in order to maintain charge neutrality relative to the centerline, what does the charge have to be on each of the plates (with a charge of -Q/2 above the left plate, and a charge of +Q/2 above the right plate)?

Chet

 

[Saitama]

Now, in order to maintain charge neutrality relative to the centerline, what does the charge have to be on each of the plates (with a charge of -Q/2 above the left plate, and a charge of +Q/2 above the right plate)?

I am honestly lost here, isn't that specifically what the question asks?

The sum of charges on the two plates should be zero so each plate must have equal magnitude of charge but how do I find this magnitude?

 

[Chestermiller]

If both charges were + Q/2, then, by symmetry, you would have no charge on either plate. If the left charge was -Q/2 and the right charge was +Q/2, then, by symmetry, charge would migrate through the wire until you had +Q/2 on the left plate and -Q/2 on the right plate. So by superposition, if you have a charge of +Q above the right plate and no charge above the left plate, the charges on the plates will be +Q/2 on the left plate and -Q/2 on the right plate.

Chet

 

[Saitama]

If both charges were + Q/2, then, by symmetry, you would have no charge on either plate.

Sorry if I am acting stupid but I can't understand why no charge appears on any plate for this case.

... So by superposition, if you have a charge of +Q above the right plate and no charge above the left plate, the charges on the plates will be +Q/2 on the left plate and -Q/2 on the right plate.

But the answer is +Q/4 on right and -Q/4 on left. :(

 

[Chestermiller]

Sorry if I am acting stupid but I can't understand why no charge appears on any plate for this case.

The two plates are connected by a wire, so the sum of the charges on them has to be zero. In the case of +Q/2 and +Q/2, you have to ask yourself how you can have a charge on either of the plates if they have to sum to zero. Which side would be positive and which side would be negative?

But the answer is +Q/4 on right and -Q/4 on left. :(

I must admit, I don't understand how this can be. I'm going to pose this to some friends, and see if they can help.

Chet

 

[Alpharup]

can you try with Gauss Law and flux consideration ?

 

[Saitama]

The two plates are connected by a wire, so the sum of the charges on them has to be zero. In the case of +Q/2 and +Q/2, you have to ask yourself how you can have a charge on either of the plates if they have to sum to zero. Which side would be positive and which side would be negative?

The following is what I think: Consider the left charge +Q/2, it tries to induce a negative charge on left plate and the right charge +Q/2 also tries to induce a negative charge on right plate but the sum must be zero and two negative values never add to zero so the only possibility is that no charge is induced, is this a correct way to think about it?

I must admit, I don't understand how this can be. I'm going to pose this to some friends, and see if they can help.

Ah, please take you time.

 

[Saitama]

Hi sharan swarup! :)

can you try with Gauss Law and flux consideration ?

I am not sure, can you please explain some more?

 

[Alpharup]

since the plate is big, we can uniform charge distribution when the placed. Conceptually speaking , equal and opposite charges are induced on the plates since they are connected. let the change induced on right plate be q. Consider an area perpendicular to both the plates including the charge. Now apply Gauss Law

 

[Chestermiller]

The following is what I think: Consider the left charge +Q/2, it tries to induce a negative charge on left plate and the right charge +Q/2 also tries to induce a negative charge on right plate but the sum must be zero and two negative values never add to zero so the only possibility is that no charge is induced, is this a correct way to think about it?

Yes.

 

[TSny]

Chestermiller's approach is very insightful and I think will lead to the right answer with a little more effort.

With the equal and opposite charges +Q/2 and -Q/2, each plate will become oppositely charged. But only if the two charges $\pm$Q/2 are very far from the center line will the charges on the plates be $\mp$ Q/2.

With the charges +Q/2 and -Q/2 in place, suppose you consider an imaginary plane that lies perpendicular to the plates and contains the line separating the plates. What can you say about the potential at points on this plane?

 

[Saitama]

Hi TSny!

With the charges +Q/2 and -Q/2 in place, suppose you consider an imaginary plane that lies perpendicular to the plates and contains the line separating the plates. What can you say about the potential at points on this plane?

The potential is zero at every point on this plane.

 

[TSny]

Yes, it would be an equipotential surface. Now imagine this imaginary vertical plane replaced by a conducting plate. Would that affect the charge induced on the original horizontal plates?

 

[Saitama]

Yes, it would be an equipotential surface. Now imagine this imaginary vertical plane replaced by a conducting plate. Would that affect the charge induced on the original horizontal plates?

I don't know.

If I place a conducting plate on the centreline, some charge is induced on it but I can't see why it should or should not affect the charge distribution on the horizontal plates.

 

[TSny]

Think about a few simpler cases. Consider an equipotential surface between two infinite parallel plates of opposite charge. If you replaced that surface with a thin conducting sheet, would it affect the electric field outside the sheet or affect the charge distribution on the original plates? Note, though, that there would be surface charge induced on the sheet.

Suppose you had a charged conducting sphere. The equipotential surfaces outside the sphere would be spherical surfaces. If you replaced one of these equipotential surfaces with a thin conducting spherical shell, would it affect the electric field (outside the shell material) or affect the charge distribution on the original conducting sphere? Again, there would be surface charge induced on the inner and outer surfaces of the shell.

In general, if you have found an equipotential surface for an electrostatics problem, then you could replace that surface with a thin conductor and not affect the fields or charge distributions in the system. But, generally, there would be surface charge induced on the surfaces of the thin conductor.

 

[Saitama]

Think about a few simpler cases. Consider an equipotential surface between two infinite parallel plates of opposite charge. If you replaced that surface with a thin conducting sheet, would it affect the electric field outside the sheet or affect the charge distribution on the original plates? Note, though, that there would be surface charge induced on the sheet.

Suppose you had a charged conducting sphere. The equipotential surfaces outside the sphere would be spherical surfaces. If you replaced one of these equipotential surfaces with a thin conducting spherical shell, would it affect the electric field (outside the shell material) or affect the charge distribution on the original conducting sphere? Again, there would be surface charge induced on the inner and outer surfaces of the shell.

No, in both the cases. So in the given case too, the charge distribution is not affected, right? But how does placing a thin conducting surface helps in this case?

 

[TSny]

Right. If you replace the equipotential surface by a conducting plate, then the charges on the original plates do not need to undergo any change in order to satisfy boundary conditions.

See if you can relate the diagrams shown.

 

[Saitama]

Right. If you replace the equipotential surface by a conducting plate, then the charges on the original plates do not need to undergo any change in order to satisfy boundary conditions.

See if you can relate the diagrams shown.

So I guess I have to use method of images now?

But why did we replace the original charge +Q with +Q/2 or are you going to come at this later?

 

[TSny]

So I guess I have to use method of images now?

But why did we replace the original charge +Q with +Q/2 or are you going to come at this later?

I don't think you need images now. Think Gauss' law.

We chose Q/2 to follow Chestermiller's superposition of the {+Q/2, +Q/2} scenario with the {-Q/2, +Q/2} scenario.

 

[Saitama]

I don't think you need images now. Think Gauss' law.

Do I select a cylinder as the gaussian surface?

 

[tiny-tim]

think biiiiiiig

 

[Saitama]

Hi tiny-tim!

think biiiiiiig

Do I have to select a bigger cylinder or my choice of gaussian surface is not correct?

 

[tiny-tim]

this whole problem is about symmetry

there's nothing symmetric about a cylinder in this context

 

[Saitama]

this whole problem is about symmetry

there's nothing symmetric about a cylinder in this context

Would a sphere or cube work?

I would like to know one thing, is this is an advanced (not sure how to define "advanced") problem or is it basic physics I am messing up with?

 

[tiny-tim]

Would a sphere or cube work?

no, i meant taking advantage of one of the basic symmetries of the whole set-up

(and remember, when you have a conductor, part of your gaussian surface is likely to be along the middle of it)

you might get a clue by working backwards from the answer … what do you need the charges to be?

I would like to know one thing, is this is an advanced (not sure how to define "advanced") problem or is it basic physics I am messing up with?

i would classify this as basic trickery

 

[Chestermiller]

It's also possible to "brute force" the solution if you know the equation for the surface charge distribution induced on an infinite flat sheet by a point charge q located at a distance h from the sheet. This would involve doing some integration. This method gives the Q/4 given results you alluded to earlier (PA), but, with the opposite signs.

So far, I for one have not been able to figure out AT's and Tiny Tim's trick method. I'm sure we are missing something very simple, but it just evades me.

Chet

 

[Saitama]

no, i meant taking advantage of one of the basic symmetries of the whole set-up

(and remember, when you have a conductor, part of your gaussian surface is likely to be along the middle of it)

you might get a clue by working backwards from the answer … what do you need the charges to be?

But if I select a gaussian surface in the middle, far from both the ends, it won't include the charge Q/2. I am honestly lost.

It's also possible to "brute force" the solution if you know the equation for the surface charge distribution induced on an infinite flat sheet by a point charge q located at a distance h from the sheet. This would involve doing some integration. This method gives the Q/4 given results you alluded to earlier (PA), but, with the opposite signs.

I am very sorry for the confusion, the given answers are indeed opposite. Sorry again.

But how do you approach it through integration?

 

[Chestermiller]

But how do you approach it through integration?

The equation for the surface charge distribution induced on an infinite flat sheet by a point charge q located at a distance h from the sheet is:
σ(x,y)=-\frac{q}{2π}\frac{h}{(x^2+y^2+h^2)^{3/2}}
where x in this equation is measured from the point directly underneath the charge. (http://www.science.org.ge/moambe/2007-vol2/bolotov.pdf)

When you have a charge of -Q/2 located at (-h,0,h) and a charge of +Q/2 located at (h,0,h), and the potential at x = 0 is equal to zero (as in our situation), you can treat the two semi-infinite sheets as a single infinite sheet. The charge distribution due to the +Q/2 charge located at (h,0,h) is given by:
σ(x,y)=-\frac{Q}{4π}\frac{h}{((x-h)^2+y^2+h^2)^{3/2}}
and the charge distribution due to the -Q/2 charge located at (-h,0,h) is given by:
σ(x,y)=+\frac{Q}{4π}\frac{h}{((x+h)^2+y^2+h^2)^{3/2}}
You just superimpose these two charge distributions and integrate over the area of the right plate (y=-∞ to y=+∞, x = 0 to x = ∞) to get the overall charge on the right plate. It should come out to -Q/4.

Chet

 

[BvU]

Well, you manage to get some hefty assistance for this cute problem. As Chet started up and Tsny and Tim brought to an end, there is a high-brow basic trickery that indeed can be pulled off here. I won't spoil T&T's fun by telling.

In textbook exercises like this, d horizontal conveniently and coincidentally happens to be equal to d vertical; never occurs in practice. I didn't even bother to explore it (meaning: kudos to T&T for making good use of it).

Coming back to my post #2 and your asking how to set up the integral in post #5:
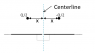
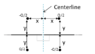
The thing I liked was that if you put the origin on the right plate right underneath Q, there is a left-right symmetry and you realize that the left plane is the same as the right plane from d to ∞.

So with ∑Q_induced= 0, whatever we find for the center strip (-d to +d) plus twice Q_{induced, left} should give 0.

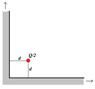
For point P = P(x,y,0) the z-component of the electric field for z > 0 (there is no E field for z in or below the plate) is $$ E_\perp = {1\over 4\pi \epsilon_0} \ {Q \over r^2 } \ \left (\hat {\rm \bf r}_1 \cdot \hat {\rm \bf k} - \hat {\rm \bf r}_2 \cdot \hat {\rm \bf k} \right ) \quad {\rm with }\enspace r^2 = x^2+y^2+d^2, \enspace{\rm and }\enspace \vec r_1 = (x, y, -d),\enspace \vec r_2 = (x, y, d), $$ so that $$ E_\perp = -{2Q\ d\over 4\pi \epsilon_0\ r^3} $$ use Gauβ $E={\sigma \over 2 \epsilon_0}$, first integrating over x from -d to d, then y from -∞ to ∞ should give -Q/2.
Chet did it, and otherwise check out MIT and UIUC Errede, in particular the helpful integrals in MIT, top p. 34.

Book answer must have sign wrong: opposite +Q a negative charge should dominate.

 

[TSny]

But if I select a gaussian surface in the middle, far from both the ends, it won't include the charge Q/2.

Try to construct a Gaussian surface that encloses the point charge and for which you know the value of E at every point on the surface.

 

[Saitama]

Try to construct a Gaussian surface that encloses the point charge and for which you know the value of E at every point on the surface.

I can't think of anything which would be useful. Selecting a sphere centred at charge won't be a good idea because the net electric field at each point on sphere is unknown owing to the charges induced on the plate. Tiny-tim said no to a cylinder. Cube probably won't work too.

I didn't really expect that this problem would get so complicated as this problem is from a high school level problem set. I thought I was missing something basic so decided to post here but looking at the above posts, I guess I was wrong. :(

 

[TSny]

I can't think of anything which would be useful. Selecting a sphere centred at charge won't be a good idea because the net electric field at each point on sphere is unknown owing to the charges induced on the plate. Tiny-tim said no to a cylinder. Cube probably won't work too.

What is the value of E inside the conductor?

Can you argue that outside the conductor and for large distances from the point charge E must fall off with distance from the point charge faster than 1/r²? If so, what does that tell you about the flux through a surface "at infinity"?

Can you construct a closed surface that is partly inside the conductor and partly "at infinity" and encloses the point charge?

I didn't really expect that this problem would get so complicated as this problem is from a high school level problem set. I thought I was missing something basic so decided to post here but looking at the above posts, I guess I was wrong. :(

I'm also surprised that it's a problem in a high school set. Seems to me that it's more at the level of Purcell's Electricity and Magnetism, a college text. But, maybe I'm not seeing a more elementary way of getting the answer!

 

[Saitama]

What is the value of E inside the conductor?

Zero.

Can you argue that outside the conductor and for large distances from the point charge E must fall off with distance from the point charge faster than 1/r²? If so, what does that tell you about the flux through a surface "at infinity"?

I honestly don't see why the field would fall that way in this case. I have seen this in the field of dipole where it falls at 1/r^3.

Can you construct a closed surface that is partly inside the conductor and partly "at infinity" and encloses the point charge?

I can't imagine how that surface could be, I have never selected gaussian surfaces of that kind.

I'm also surprised that it's a problem in a high school set. Seems to me that it's more at the level of Purcell's Electricity and Magnetism, a college text. But, maybe I'm not seeing a more elementary way of getting the answer!

Ah, I do have the book btw (which I bought during my short appearance at college, now I am back to high school stuff ).

Here is the source of problem: http://www.komal.hu/verseny/feladat.cgi?a=honap&h=201401&t=fiz&l=en

 

[Chestermiller]

Can you construct a closed surface that is partly inside the conductor and partly "at infinity" and encloses the point charge?

Hi TSny. The part I'm having trouble with in applying Gauss's law is what to do about the vertical zero potential surface. Even though the component of the electric field tangent to this surface is zero throughout the surface, the electric field is normal to the surface and is a function of position on the surface. Do you have in mind replacing the surface with an equivalent conducive sheet, with positive and negative charges on the opposing surfaces of the sheet? I'm not confident about doing something like that, given my limited experience with electrostatics.

Chet

 

[TSny]

Hi TSny. The part I'm having trouble with in applying Gauss's law is what to do about the vertical zero potential surface. Even though the component of the electric field tangent to this surface is zero throughout the surface, the electric field is normal to the surface and is a function of position on the surface. Do you have in mind replacing the surface with an equivalent conducive sheet, with positive and negative charges on the opposing surfaces of the sheet? I'm not confident about doing something like that, given my limited experience with electrostatics.

Yes, we add a vertically conducting plate as shown in the third figure attached.

In the three figures shown, the electric field in the first quadrant is the same for each figure. In the figure on the left, the charge induced on the portion of the horizontal plate where x > 0 is the same as for the right figure.

Also, due to symmetry in the third figure, you can compare the charge on the vertical plate to the charge on the horizontal plate.

Using Gauss' law you can determine the total charge induced on both the horizontal and vertical plates in the third figure. [EDIT: Note that you can choose parts of the Gaussian surface to lie in the xy horizontal plane and the yz vertical plane where it may be considered to be inside conducting material.]

 

[TSny]

Zero.

Yes.

I honestly don't see why the field would fall that way in this case. I have seen this in the field of dipole where it falls at 1/r^3.

Look at the middle figure that I posted in #44. Far from the charges, would the field be that of a point charge, a dipole, a quadrupole, or something else?

I can't imagine how that surface could be, I have never selected gaussian surfaces of that kind.

A hint is given in the "Edit" of my post #44. Choose part of the surface to be flat and lying in the horizontal xy plane for x>0. Another part will be flat and lying in the vertical yz plane for z>0. You will need to add more parts to make a closed surface and decide how big to make the whole thing.

Ah, I do have the book btw (which I bought during my short appearance at college, now I am back to high school stuff ).

Here is the source of problem: http://www.komal.hu/verseny/feladat.cgi?a=honap&h=201401&t=fiz&l=en

Nice problems. In my opinion, some of these are definitely more advanced than typical high school physics problems in the United States. But then, we all know that Hungarians are from Mars

 

[ehild]

Here is the source of problem: http://www.komal.hu/verseny/feladat.cgi?a=honap&h=201401&t=fiz&l=en

That is Hungarian! I used to solve problems written in that Journal when at high school, more than half century ago... Those problems are very cunning and are for the best students.

I would solve it as follows, see attachment. The charge Q induces -Q surface charge on the upper surface of the plates. The plates are divided into strips, the surface charge densities are q₂ on the left plane, q₁ in the strips symmetric to the charge Q, between x=0 and x=±D, and q₂ on the rightmost strip. q₁+q₂=-Q/2

You get q₁ by integrating ε₀ in the range 0<x<D, -∞<y<∞. Integrate with respect to y first. The following integral is helpful (from Wolframalpha)

\int{\frac{1}{(\sqrt{y^2+a^2})^3}dy}=\frac{y}{a^2\sqrt{y^2+a^2}}dy

The total charge of the connected plates is zero. Because of the induced charge on the upper surfaces, there is surface charge on the back surfaces, too. The back surface charge is evenly distributed. The plates are of equal size. So the total charge of the left plate is q₂+Q/2 and the charge of the right plate is 2q₁+q₂+Q/2.

ehild

 

[BvU]

@ehild: You agree that the Hungarian "solution" is wrong by a factor of -1 ?

Re your integral: could you show us how to integrate wrt y first ? I find it rather awkward...

 

[Chestermiller]

Yes, we add a vertically conducting plate as shown in the third figure attached.

In the three figures shown, the electric field in the first quadrant is the same for each figure. In the figure on the left, the charge induced on the portion of the horizontal plate where x > 0 is the same as for the right figure.

Also, due to symmetry in the third figure, you can compare the charge on the vertical plate to the charge on the horizontal plate.

Using Gauss' law you can determine the total charge induced on both the horizontal and vertical plates in the third figure. [EDIT: Note that you can choose parts of the Gaussian surface to lie in the xy horizontal plane and the yz vertical plane where it may be considered to be inside conducting material.]

Thanks TSny. I've finally gotten the idea of how to do it. But I would have set it up a little differently than you have done it. With reference to your figures, in the first figure, our starting point is with the charges equal to -Q/2 and + Q/2. I would then have represented this figure as the sum of two other figures: (figure 1). Your middle figure with Q/4 s, and the signs on the charges the same as in your figure, plus (figure 2). Your middle figure with Q/4 s, but with both positive charges on the right and both negative charges on the left.

Because of symmetry, the setup in (figure 1) would not give rise to any net induced charges on the two plates. But, the setup in (figure 2) would give rise to the same total induced charges on the plates as in the original problem. Also, in (figure 2), the charges on the upper and lower surfaces of each plate would be identical, and the electric fields within the plates would be zero. I would then place a vertical plate on the same vertical zero-potential surface that you have used in your third figure. This plate would develop an induced negative charge on its right surface and an induced positive charge on its left surface. The electric field within this plate would be zero, and the charge distribution on the right side of the plate would be identical to the charge distribution on the upper surface of our right plate. This would represent my third figure. I would put one Gaussian planar surface down the middle of the right plate, another Gaussian planar surface up the middle of the vertical plate, and a third Gaussian surface at infinity. So, my third figure would look essentially identical to yours. But the point charge would be +Q/4, only half the charge on the right plate would be included within the Gaussian surface, and only the negative charge on the vertical plate would be included (and this would equal the charge on the upper surface of the right plate). If q was half the charge on the negative plate, then by applying Gauss's law, q = -Q/8. So, the full charge on the right plate would be -Q/4.

I hope this makes some kind of sense. It was very hard to describe in words. If you were able to understand my description, does this work for you?

Chet

 

[TSny]

I hope this makes some kind of sense. It was very hard to describe in words. If you were able to understand my description, does this work for you?

Chet, I'm pretty sure I followed your logic and it looks correct to me. Nice!

 

[ehild]

@ehild: You agree that the Hungarian "solution" is wrong by a factor of -1 ?

Re your integral: could you show us how to integrate wrt y first ? I find it rather awkward...

The solution in Hungarian

A bal oldali lemezen Q/4, a jobb oldalin -Q/4 lesz a töltés.


means

'The charge on the left plate will be Q/4, that on the right plate will be -Q/4.'

(bal =left, jobb = right) The Hungarian solution is correct.

Applying the method of mirror charges, the electric field on the upper surface is normal to the plate, pointing downward, and

E_z=-\frac{1}{2\pi\epsilon_0}\frac{Q D }{(x^2 + y^2 + D^2)^{3/2} }

The induced charge q1 is the integral of σ=ε₀E_z for the orange strip

q_1=-\int_{-\infty} ^{\infty}\int_0^D{\frac{1}{2\pi}\frac{Q D }{(x^2 + y^2 + D^2)^{3/2} }dydx}

apart from the constant factors, the integrand is of the form \frac{1}{(y^2 + a^2)^{3/2}}
with a^2=x^2+D^2.

The integral is shown in my last post.

ehild