- #1
Saladsamurai
- 3,020
- 7
[SOLVED] Charges are Great! Need more assistance!
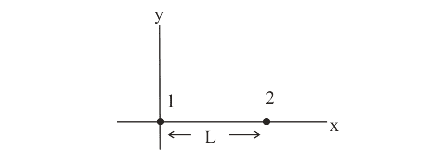
In the figure particle 1 of +q and particle 2 of charge +4q are held at a separation of L=.09 m If particle 3 of charge q_3 is to be placed such that the three particles remain in place when released, what must be (a) the ratio q_3/q and the (b) x and (c) y components?
Okay, I solved b and c easy enough. There is no y component and x=.03.
I am having trouble with a. Any hints? I know it must be a similar procedure, that is, I need to use the fact that there is NO NET force...but I can't seem to spot the correct relationship such that I am left with the desired variables (they don't cancel).
Word.
Homework Statement
In the figure particle 1 of +q and particle 2 of charge +4q are held at a separation of L=.09 m If particle 3 of charge q_3 is to be placed such that the three particles remain in place when released, what must be (a) the ratio q_3/q and the (b) x and (c) y components?
Okay, I solved b and c easy enough. There is no y component and x=.03.
I am having trouble with a. Any hints? I know it must be a similar procedure, that is, I need to use the fact that there is NO NET force...but I can't seem to spot the correct relationship such that I am left with the desired variables (they don't cancel).
Word.