4real4sure said:
I tried to do it several times based on may understanding but for some reason I am so not able to reach to the solution. Any hint?
Let's start with the first part (a).
For each charge
Q at the bottom, you can find the
magnitude of the force from that particular charge on charge
q using
\vec F = \frac{1}{4 \pi \varepsilon_0} \frac{qQ}{r_2} \hat \imath_r.
where \hat \imath_r points in the direction from the particular
Q to
q.
But the \hat \imath_r for one charge is different from the \hat \imath_r of the other charge, because they point in different directions. So you can't just add them simply. For each case, you need to break up \hat \imath_r into its \hat \imath_x and \hat \imath_y components.
That might involve something like
F_x = F\cos \theta
F_y = F \sin \theta
(This relationship is just for example purposes, the particular relationship may depend on the particular problem/particular pair of charges).
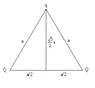
Or if you don't want to use trigonometric functions, you can do it using the Pthagorean theorem (which works with this problem). If
a is the side of an equilateral triangle, and you vertically bisect the triangle down the middle, forming two isosceles triangles, then the base of each isosceles triangles is
a/2. What does Pthagorean theorem tell you about the height of the triangle relative to
a?