- #1
AdityaDev
- 527
- 33
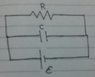
The cell can provide conatant emf ε and initial charge of capacitor is zero.
Now current through resistor initially is zero and increases. But the potential difference across the capacitor is always a constant with magnitude ε.
then ##\frac{q(t)}{C}=E##
So ##q(t)=CE## which implies q is constant and non zero. So initial charge in capacitor can never be zero! But this contradicts the initial condition. What mistake am I doing? I am trying to find the time constant.
Now current through resistor initially is zero and increases. But the potential difference across the capacitor is always a constant with magnitude ε.
then ##\frac{q(t)}{C}=E##
So ##q(t)=CE## which implies q is constant and non zero. So initial charge in capacitor can never be zero! But this contradicts the initial condition. What mistake am I doing? I am trying to find the time constant.