bobg123
- 1
- 0
- Homework Statement
- Find input impedance of the circuit shown. Calculate impedance between the input terminal and the ”ground”. Two resistors R1 have equal resistance.
- Relevant Equations
- V-=V+
V=IR
V_out=-R1/R3 Vin
V_out=R1/R2+1 Vin
I've been given the following circuit and have been asked to find the input impedance and the impedance between the input terminal and ground. I've never encountered an operational amplifier configured like this.
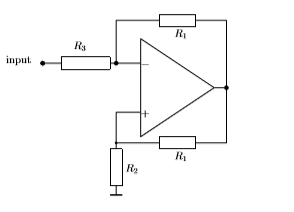
I know that the voltages at the - and + terminals of the op amp are ideally equal. In a normal inverting/non inverting op amp, I've been told the voltages at those points are zero. Is this still the case? If so, what is the output voltage? I'm having trouble conceptually understanding what this particular circuit does.
I'm not sure how to approach this problem, but I've tried separating the circuit into an inverting and non-inverting circuit. For the inverting circuit, I know V_out=-V_in*R1/R3. This gives me V(-)=V_in+V_in/R_3. For the noninverting, I know V_out=(R1/R2+1)V_in. The voltage at V(+) should be equal to V(-), giving V_in+V_in/R_3=V(R1)-V(R2)=R1/R2V_in+V_in-V(R2). Some rearrangement gives me V_in(1/R3-R1/R2)=-V(R2). Is this the right way of approaching the problem? Where do I go from here to calculate the impedance?
I know that the voltages at the - and + terminals of the op amp are ideally equal. In a normal inverting/non inverting op amp, I've been told the voltages at those points are zero. Is this still the case? If so, what is the output voltage? I'm having trouble conceptually understanding what this particular circuit does.
I'm not sure how to approach this problem, but I've tried separating the circuit into an inverting and non-inverting circuit. For the inverting circuit, I know V_out=-V_in*R1/R3. This gives me V(-)=V_in+V_in/R_3. For the noninverting, I know V_out=(R1/R2+1)V_in. The voltage at V(+) should be equal to V(-), giving V_in+V_in/R_3=V(R1)-V(R2)=R1/R2V_in+V_in-V(R2). Some rearrangement gives me V_in(1/R3-R1/R2)=-V(R2). Is this the right way of approaching the problem? Where do I go from here to calculate the impedance?