Circuit Quesiton Homework: Node Voltage Method | Attempted Solution

[GreenPrint]

Homework Statement

See Attachment

Homework Equations

The Attempt at a Solution

I know how to do A this is an easy question. I'm not sure how to do B.

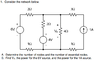
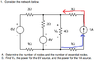
For A there are two essential nodes. There are seven nodes.

For B I'm not sure. I always drew my current so that way it went from positive to negative (this is after all the direction of current I believe). This creates a problem because when I try to solve the problem using the node voltage method I get about 1.714 for the top essential node which I'm not sure if it's right or anything but it seems a little bit off.

I don't understand why the right most branch with the current source... why is it that the whole branch is regulated to be 1 A even before the current source and before the 1 ohm resistor but after the node? This never made much sense to me.

I am also not sure how to solve using the node voltage method because I called the top essential node node voltage 1

(V1 - 6)/2

is a correct way to the difference in voltage between V1 and the bottom essential node for the reference node which I put a ground. At least I think it is but I'm not sure how to deal with the 1 ohm resistor before the 6V voltage source in my calculations.

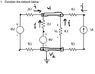
Check the second attachment for my drawings of current etc.

As you can see all the currents go into the top essential node which is a problem.

Thanks for any help at all.

 

[phinds]

I don't understand why the right most branch with the current source... why is it that the whole branch is regulated to be 1 A even before the current source and before the 1 ohm resistor but after the node? This never made much sense to me.

Huh? It seems like you're saying "well, I have a current source but I don't understand why I have a current source" Can you restate your question?

 

[GreenPrint]

Done Editing

Ya

I understand why the red line is 1 A as it comes after the source. I however don't understand why before the current source (the blue line) is also one amp, as it comes before the current source.

see attachment

 

[phinds]

Done Editing

Ya

I understand why the red line is 1 A as it comes after the source. I however don't understand why before the current source (the blue line) is also one amp, as it comes before the current source.

see attachment

Uh ... because it is in the same serial path and could not possibly be anything else? How could you possibly have one current leaving a wire and a different current entering the wire?

 

[GreenPrint]

hm I've never thought about it like that lol

um can you help me with part B? I think I got the direction of the currents messed up as well lol

 

[phinds]

hm I've never thought about it like that lol

um can you help me with part B? I think I got the direction of the currents messed up as well lol

There is no such thing as getting the direction of the currents messed up. Just draw them however you draw them and if they go the other way you'll get a negative answer for anyone that does.

 

[GreenPrint]

Can I combine the resistors in the left most branch (the one with the 6V power source and two resistors 2 ohm, 1 ohm) into an equialent one ohm resistor of 3 ohm? I'm not sure if I can or not because of the power source inbetween them.

I have identified the current in the second branch (the one with the 4V source and the 2 ohm source) as 2 A.

 

[NascentOxygen]

Can I combine the resistors in the left most branch (the one with the 6V power source and two resistors 2 ohm, 1 ohm) into an equialent one ohm resistor of 3 ohm?

Yes, resistances in series simply add.

I have identified the current in the second branch (the one with the 4V source and the 2 ohm source) as 2 A.

You are not able to calculate this current, because you haven't determined the voltage at the "top" of that 2Ω resistor. Until you know the voltage at both ends of that resistor, you can't say what is the potential difference across it. (As you will see, only if Vx=0 will your current in that second branch be 2 A. )

 

[GreenPrint]

Start from the left and number the 4 branches from 1 to 4

The second branch
\frac{V_{1}-4}{2}
The third branch
\frac{V_{1}}{4}
The first branch
\frac{V_{1}-6}{3}
The fourth branch
\frac{V_{1}}{4}

\frac{V_{1}-4}{2} + \frac{V_{1}}{4} + \frac{V_{1}-6}{3} + \frac{V_{1}}{4} = 0
6V_{1}-24+3V_{1}+4V_{1}-24+3V_{1}=0
16V_{1}=48
V_{1}=3 V

I feel as if this answer might be wrong for V_{1} as my friend said he got different answers to the questions in part B. Is it wrong? I don't see what I'm doing wrong here. I thought about just counting 1 amp as the current in the fourth branch due to the current source. But then...

\frac{V_{1}}{4}=1, V_{1}=4 V

I'm not sure which answer is right if any of them. Thanks for your help. Also thanks for helping me before in that other circuit problem. I ended up getting the right answer and checked that I got the same answers as several other people in my class. You were big help.

 

[NascentOxygen]

The current in the 4th branch is indeed 1 amp. It is determined by a current source, and is not a function of V1. (You don't know the voltage across that current source, at this stage, and you are not asked to find it.)

Now, write the expression for the sum of the currents into that node where you labelled V1. The sum of all currents into a node always = 0.