Circuits with series and parallel wiring

AI Thread Summary
The discussion focuses on calculating the equivalent resistance of four identical 5.00 Ω resistors arranged in a square configuration. For part (a), the resistance between points A and B is determined to be 3.75 Ω, while for part (b), the resistance between points A and C is 5.00 Ω. Participants emphasize the importance of understanding series and parallel resistor combinations to solve these problems. Suggestions include researching equivalent resistance concepts in textbooks or online resources for clarity. Mastering these calculations is essential for accurately analyzing circuit configurations.
r_swayze
Messages
65
Reaction score
0
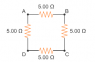
Four identical 5.00 Ω resistors are joined and form the four sides of a square. (a) What is the resistance between points A and B? (b) What is the resistance between A and C?

The answer to (a) is 3.75 and (b) is 5, but I have no idea how to get those answers. Can somebody help?
 

Attachments

  • Capture.PNG
    Capture.PNG
    2.3 KB · Views: 516
Physics news on Phys.org
Do you know the equivalent resistance of the series and parallel combination of resistances? It not, search the web or the textbook.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

How to determine if electrical components are connected in parallel or in series?
Replies
10
Views
901
Current through an inductor as a function of time
Replies
10
Views
318
Electrical Circuits - Parallel vs. Series
Replies
14
Views
1K
Optimum Battery (and Wire) to Power 10x Mini 1.5V Bulbs in Parallel?
Replies
6
Views
2K
Is This a Series or Parallel Circuit?
Replies
13
Views
897
Understanding example in Wikipedia entry for open circuit voltage
Replies
3
Views
2K
Equivalent resistance of a circuit
Replies
3
Views
2K
Worst-case power consumed by a circuit with MOSFETs
Replies
2
Views
920
Finding the Optimal Combination of Resistors for a Desired Total Resistance
Replies
9
Views
2K
Using Kirchhoff's Rule - Theory question
Replies
8
Views
2K

Hot Threads

Recent Insights

Back
Top