Classical Relativity and Speed of Sound

[Ericv_91]

Homework Statement

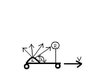
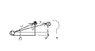
It is well known that the speed of sound in air is u = 330m/s at STP. What this means is that sound travels at speed u in all directions in the frame S where the air is at rest. In any other frame S', moving relative to S, its speed it not u in all directions. To verify this, some students set up a loudspeaker L and receiver R on an open flatcar, as in the figure that I hopefully successfully attached; by connecting an oscilloscope, they can measure the time for a sound to travel from L to R and hence find its speed u' (relative to the car). a) Derive an expression for u' in terms of u, v, and theta', where v is the car's speed through air, and theta' is the angle between V and LR. [Hint: Draw a velocity-addition triangle to represent the relation u = u' + v. The law of cosines should give you a quadratic equation for u'.]

Homework Equations

a²= b²+c²-2bc*cosA

The Attempt at a Solution

I'm having a lot of trouble with this problem as I don't think that I can even get the picture of it right. Hopefully the picture properly attached to show what I think is going on. I understand that the speed of sound will be moving faster since its under the cart, and that it won't be able to go directly to the receiver since the receiver will also be moving. It must go at a slightly smaller angle, right? I attempted to use the cosine law and solve for u', but when I looked at the answer in the back of the book, I was confusingly surprised. The answer stated at the back is: u'= sqrt[(u^2)-(v^2)(sin^2(theta'))] - v*cos(theta'). So, I don't need the answer... But how the heck did they get that answer? How did they get sin into the law of cosine? I don't know. Any help is greatly appreciated.

Eric

 

[Delphi51]

If you apply the law of cosines to the second diagram calling the side marked v as side a, the u side b and the u' side c, you get
v² = u'² + u² - 2uu'cosθ.
Rearranging this into the form a*u'² + b*u' + c = 0 you can use the quadratic solution to get an expression for u'. With a bit of work, including use of cos² - 1 = -sin², I get an expression that includes the answer you quote . . . plus another term. Maybe you'll have better luck with it, or maybe something is missing from the answer. Both answers work when v = 0, θ = 0, making u = u' as it should.