Pouyan
- 103
- 8
- Homework Statement
- Derive the Clausius' theorem
- Relevant Equations
- Qh/Ql= Th/Tl
ΔW= ΣdQi
I see this in my book but there is something I don't get!
If we consider a Carnot cycle where heat Qh enters and heat Ql leaves,
We know Qh/Ql=Th/Tl
And we define ΔQ_rev then :
∑(ΔQ_rev/T) = (Qh/Th) - (Ql/Tl) =0
I insert an image:
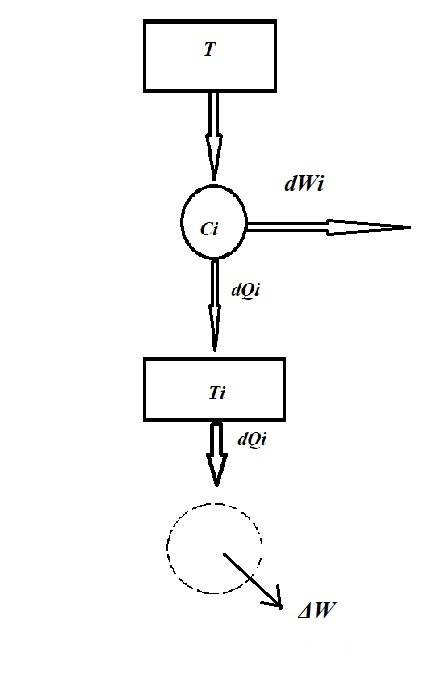
Which shows the heat dQi entering the reservoir at Ti from a reservoir at temperature T via a Carnot (Ci).
We know:
heat to reservoir at Ti / Ti = heat from the reservoir at T/ T
So : dQi/Ti = (dQi+dWi)/T
and rearranging:
dWi=dQi((T/Ti) -1)
The system in the image seems to convert heat to work but it cannot convert 100% of heat to work according to Kelvin's statement of the second law and hence we must insist that this is not the case. Hence:
Total work produced per cycle = ΔW + ∑(dWi) =< 0
But there is something I don't understand!
ΔW = ∑(dQi)
and dWi=dQi((T/Ti) -1)
So the total work produced per cycle = T ∑(dQi/Ti)
But why we say that this is less or equal than zero ?
T ∑(dQi/Ti) =< 0
T > 0.
Ti must be more than zero of course (Ti > 0)
How can we say that dQi =< 0 ?
Is that because it leaves from the reservoir with lower temperature ?
If we consider a Carnot cycle where heat Qh enters and heat Ql leaves,
We know Qh/Ql=Th/Tl
And we define ΔQ_rev then :
∑(ΔQ_rev/T) = (Qh/Th) - (Ql/Tl) =0
I insert an image:
Which shows the heat dQi entering the reservoir at Ti from a reservoir at temperature T via a Carnot (Ci).
We know:
heat to reservoir at Ti / Ti = heat from the reservoir at T/ T
So : dQi/Ti = (dQi+dWi)/T
and rearranging:
dWi=dQi((T/Ti) -1)
The system in the image seems to convert heat to work but it cannot convert 100% of heat to work according to Kelvin's statement of the second law and hence we must insist that this is not the case. Hence:
Total work produced per cycle = ΔW + ∑(dWi) =< 0
But there is something I don't understand!
ΔW = ∑(dQi)
and dWi=dQi((T/Ti) -1)
So the total work produced per cycle = T ∑(dQi/Ti)
But why we say that this is less or equal than zero ?
T ∑(dQi/Ti) =< 0
T > 0.
Ti must be more than zero of course (Ti > 0)
How can we say that dQi =< 0 ?
Is that because it leaves from the reservoir with lower temperature ?