Will M
- 8
- 0
[SOLVED] Coefficient of friction on an inclined plane
The problem I have is to determine the coefficient of kinetic friction between two wooden objects, a block and a ramp, using the fewest measurements possible. The initial velocity will be 0. I can measure the angle of incline, the distance traveled along the ramp, the time taken, but should not have to measure mass. I do not currently have any values, but should create an equation. Can I do this, and if so, am I on the right track?
Fnet = ma
Ff = μFN
Δd = V1Δt + ½aΔt²
Fnet = ma
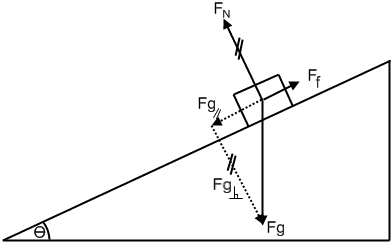
Ff - Fg║ = ma
Ff - Fg sin θ = ma
Ff - mg sin θ = ma
Ff = 2Δd/Δt² - g sin θ
μFN = 2Δd/Δt² - g sin θ
μFg┴ = 2Δd/Δt² - g sin θ
μFg cos θ = 2Δd/Δt² - g sin θ
μ = [(2Δd/Δt²) - g sin θ] / Fg cos θ
μ = [(2Δd/Δt²) - g sin θ] / mg cos θ
Note:The substitution of acceleration for 2Δd/Δt² in the 5th line is from the equation Δd = V1Δt + ½aΔt² where V1Δt evaluates to 0.
Homework Statement
The problem I have is to determine the coefficient of kinetic friction between two wooden objects, a block and a ramp, using the fewest measurements possible. The initial velocity will be 0. I can measure the angle of incline, the distance traveled along the ramp, the time taken, but should not have to measure mass. I do not currently have any values, but should create an equation. Can I do this, and if so, am I on the right track?
Homework Equations
Fnet = ma
Ff = μFN
Δd = V1Δt + ½aΔt²
The Attempt at a Solution
Fnet = ma
Ff - Fg║ = ma
Ff - Fg sin θ = ma
Ff - mg sin θ = ma
Ff = 2Δd/Δt² - g sin θ
μFN = 2Δd/Δt² - g sin θ
μFg┴ = 2Δd/Δt² - g sin θ
μFg cos θ = 2Δd/Δt² - g sin θ
μ = [(2Δd/Δt²) - g sin θ] / Fg cos θ
μ = [(2Δd/Δt²) - g sin θ] / mg cos θ
Note:The substitution of acceleration for 2Δd/Δt² in the 5th line is from the equation Δd = V1Δt + ½aΔt² where V1Δt evaluates to 0.