Righthanded123
- 4
- 0
Homework Statement
The problem asks to find out whether the rod yields at points in section A according to the tresca and von mises criteria
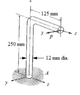
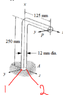
P is 120N
Homework Equations
Shear stress= VQ/It
Stress= Mx/I
shear stress= Tp/J
The Attempt at a Solution
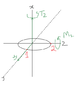
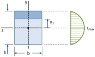
I picked 2 points at section A.
The first point is on the
I calculated that P will cause a shear stress Vy along the Y axis which is -120N
P will cause a bending moment Mz about the z axis 120N x 250mm
and P will cause a torque Tx about the x-axis 120N x 125mm
At point 1
Vy will not cause a shear stress because Q=0
Tx will cause a shear stress using Tp/J
and Mz will cause a compressive stress which will be at a maximum
Then i found the principal stresses using the mohr circle method
Then using the von mises and tresca criteria I compared the stresses to the yield stress of 200MN/mm to determine if the rod will yield.
At point 2
Vy will case a shear stress found by VQ/It
Tx will cause a shear stress using Tp/J
and Mz will not cause a normal stress because the distance from neutral axis for point 2 is 0 ?
This where I am stuck I am not sure point 2 only has shear stresses as I have calculated
and If i have picked enough points, as i imagine it will be the same values.