Computing AC voltage in a complex filter

[Xaras]

Homework Statement

Computing AC voltage

Relevant Equations

cut off frequency, ac voltage.

Problem Statement: Computing AC voltage
Relevant Equations: cut off frequency, ac voltage.

Hey guys,

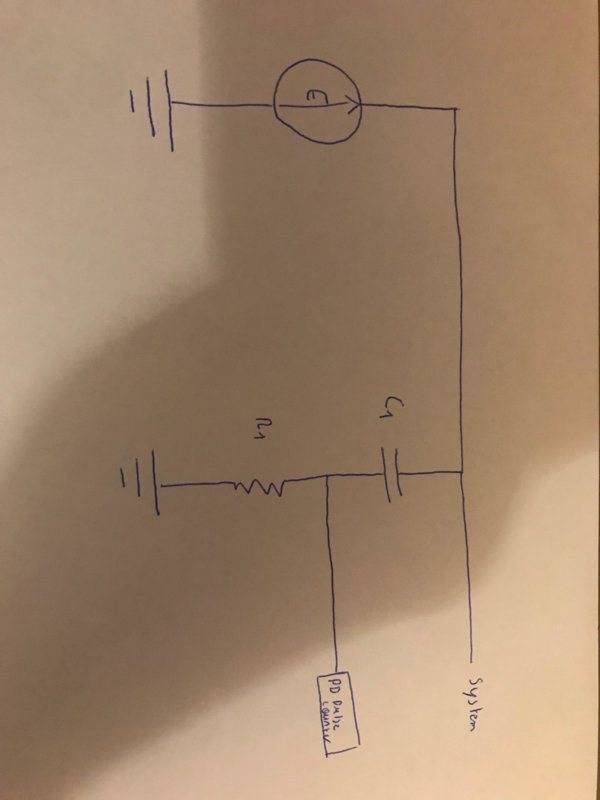
Amazing to be in this group ! Please find attached the diagram of the problem.

E = 10kV at 60Hz, C1 = 60pF and R1 = 1k.

I have to compute the ac voltage in reference to ground at point [1]. Does it means that I need to compute the voltage at the resistance or the capacitor ? I was thinking it's the the voltage drop between the ground and the resistance, so here is my solution :

Vr(w) = R1/(ZC1(w) + R) * E(w) = 1/(1+jR1C1w)*E(w).

Then I have to compute the cut off frequency, as this is a RC classical scheme,fc = 1(2*π*R*C) right ?

Thanks for the help !

 

[BvU]

Hello Xaras, $\qquad$ $\qquad$ !

Seems like you got it all nicely sorted out. But next time don't orient the picture sideways: my neck still hurts !

Your analysis corresponds to e.g. what we see https://www.electronics-tutorials.ws/filter/filter_3.html, so I think you are doing OK.

 

[DaveE]

So, in your solution, for a fixed magnitude of E(w), as w increases you would have Vr decreasing. Is this what you would expect with a circuit like this? How does the impedance of a capacitor change with frequency?

 

[Xaras]

I was just hesitating because I thought current was flowing to the system and to the PD pulse counter so we can't apply the theorem.

But thanks for your answer :) !

 

[Xaras]

So, in your solution, for a fixed magnitude of E(w), as w increases you would have Vr decreasing. Is this what you would expect with a circuit like this? How does the impedance of a capacitor change with frequency?

I didn't get what you wanted to say ...

 

[Xaras]

By the way I forgot to put the numbers on the picture, here they are ...

 

[DaveE]

It is usually a good idea to check your final answer somehow to verify that there isn't a mistake. In simple AC circuits this is often done by looking at the behavior at different frequencies. In the world of engineering it is often not good enough to work through your equations and declare victory without checking them somehow. People make mistakes all the time, good engineers find and fix their own mistakes.

 

[Xaras]

Yes sure,

So here are the answers for the cut off frequency = 1/(2*pi*R*C) = 2653 kHz.

For the Vr(w) = 10000/(1+ 2.26*10^(-5)*j).

Is it right ?

 

[DaveE]

Ok, the subtle approach isn't working. Your method is correct but your final formula is not. Try again. Remember that ZC1(w)=1/(jwC1).
Also note that capacitors tend to pass high frequencies through with low impedance but block lower frequencies because their impedance is higher at low frequencies. So a circuit like this will have more voltage on the resistor when the source frequency is higher than if the frequency is lower. Your final solution should reflect that behavior.

 

[DaveE]

BTW, your solution is correct for the voltage across the capacitor, so you are close.

 

[Xaras]

Ok, the subtle approach isn't working. Your method is correct but your final formula is not. Try again. Remember that ZC1(w)=1/(jwC1).
Also note that capacitors tend to pass high frequencies through with low impedance but block lower frequencies because their impedance is higher at low frequencies. So a circuit like this will have more voltage on the resistor when the source frequency is higher than if the frequency is lower. Your final solution should reflect that behavior.

Let's do it again. Here the goal is to compute the voltage across the resistor.

So :

Vr(w) = R1 * E(w) / (R1 + ZC1) = R1 * E(w) / ( R1 + 1/jC1w) = (E*R1*C1*jw)/(1+ jR1C1w).

 

[Xaras]

There is something that I don't get, we're in low frequency. So Xc -> infinite = > Zc = 0 right ?
So it means that Vr(w) = E(w) ?

 

[DaveE]

Let's do it again. Here the goal is to compute the voltage across the resistor.

So :

Vr(w) = R1 * E(w) / (R1 + ZC1) = R1 * E(w) / ( R1 + 1/jC1w) = (E*R1*C1*jw)/(1+ jR1C1w).

Yes, good work!
BTW, an alternate form: Vr(w) = E(w)⋅[1/(1+1/(jwRC))] is sometimes easier to compute. But they are the same thing, it's just a matter of personal preference.
I kind of like the symmetry in these solutions:
Vc=E⋅[1/(1+(jwRC)]
Vr=E⋅[1/(1+1/(jwRC))]=E⋅[jwRC/(1+(jwRC)]
Then note that Vc+Vr = E⋅[1/(1+(jwRC)] + E⋅[jwRC/(1+(jwRC)] = E⋅[(1+jwRC)/(1+(jwRC)] = E as it should be.
This is one of many ways to check your solutions.

 

[DaveE]

No, Zc is never zero or infinite. That is just the way they tend as the frequency approaches zero or infinity. In fact frequency is never zero or infinity in a rigorous sense. For example, even a DC circuit (which everyone, including me, says has f=0), really is just very very close to zero. If you turn that circuit on and off once a day then f=1/day.
Consider this original circuit at 60Hz, |Zc|=44.2 Mohm = 44.2e6 ohm, this is so much larger than the value of R=1 Kohm that, in practice, you might approximate it as infinite, then all of the voltage from E is across C1 (with an error of about 1/44.2e3 = 0.0023%. But if R=10 Mohms that wouldn't be a good approximation anymore, because 44.2 Mohms isn't much larger than 10 Mohms.
So when people talk about impedances being essentially zero or infinite it is always in relation to the other impedances in the circuit (although they often don't say that explicitly).
This, BTW, is why people want to know the cut-off frequency. In a simple circuit like this if the frequency of your source is very far away from the cut-off frequency then you can make approximations like this. Near the cut-off frequency the pertinent circuit elements all matter.
Don't worry if your not following all of this, it will become more clear as you study circuits more. However, for simple circuits like this one, it will really help in your studies if you spend a bit of time thinking about what the different parts of the circuit are doing after you have calculated your answer. You can spot errors and also learn to get a feeling for what to expect in similar problems later.

 

[DaveE]

Also, you can look at the current, I(w)=E(w)/Z(w) where
Z(w)=R+1/(jwC)=(1+jwRC)/(jwC).
Then as w→0, Z→∞, I→0. This corresponds to assuming that Zc=∞
as w→∞, Z→R, I→E/R. This corresponds to assuming that Zc=0

 

[BvU]

Tanks Dave, I overlooked the math error in

Vr(w) = R1/(ZC1(w) + R) * E(w) = 1/(1+jR1C1w)*E(w)

$$ V_{R_1}(\omega) = {R_1\over Z_{C_1}(\omega ) + R_1} * E(\omega) \quad \stackrel {\bf ?} {=} \quad {1\over 1+jR_1 C_1\omega}*E(\omega ) $$

( I must be too spoiled by the good looks of $\LaTeX$ to see mistakes in non-typeset equations )