daphnelee-mh said:
but the question needs us to prove that it will return to equilibrium
Daphne,
I have been researching a little about this problem.
As I have told you earlier, that concept of using a small pulley for a cable hoisting a truss is something that I have never seen in many years of working in construction and I believe it can't work.
Any type of sling has eyes at both extremes for connecting it to the hook of the crane or to shackles or to any other rigging hardware.
One of the purposes of those eyes is to avoid accidental tipping of the loads and/or destructive slides of the sling over metal.
Please, see:
https://www.mazzellacompanies.com/R...est-sling-hitch-vertical-basket-choker-bridle
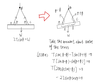
Again, once the load is accidentally placed in a tipped position and that pulley has allowed the cable to slide through it, making leg BA longer than leg BC (as shown in your solution), the load can't return to the horizontal position by itself.
For any tipped position of the truss, its center of mass will be located directly below the hook of the crane, along a vertical line.
If we assume that the CM is located midpoint of the truss, we could call point D to the intersection of that vertical line and side AC of your triangle ABC.
We can consider the distance between vertex B (location of pulley) and point D to be the median of the triangle.
Apollonius's theorem seems to demonstrate that the median of the triangle will increase as lengths of sides BA and BC become different.
##AD=\sqrt{[(AB^2+AC^2)/2]-BD^2}##
That will relocate the CM of the truss lower (respect to its position when truss was horizontal), to a point of less potential energy.
With the hook keeping its spatial position, the extreme situation could be a close to vertical position of the truss and the lowest location of CM.
Because of that, additional external work would be necessary to return the truss to the horizontal position.
Please, see:
https://en.wikipedia.org/wiki/Median_(geometry)
If you have time, also take a look at page 53 (sling configurations) of the following document:
https://www.oshatrain.org/courses/pdf/HoistingRigging_Fundamentals.pdf