Conceptual Question- Hydrostatic Pressure

[bcjochim07]

b]1. Homework Statement [/b]
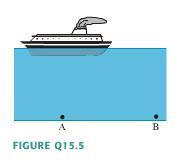
In the figure, is pressure at A larger than, smaller than, or equal to the pressure at B?

[

Homework Equations

The Attempt at a Solution

My first instinct is that they are equal because they are at equal heights, but then again, isn't the pressure at the surface above A greater than the surface above B because of the force, mg, of the boat exerted over the surface area in addition to the pressure exerted by the atmosphere? Could someone please explain this to me? Thanks.

 

[Shooting Star]

You have mentioned equal heights -- height above what? I hope you meant depth from the surface of the water. Then the pressures must be equal, since the depths are equal.

But there's a ship above A. Your concern is will that change the pressure at A? (You can safely neglect atmospheric pressure, since that is acting everywhere.)

The ship exerts some pressure on the water surrounding it due to its weight. It also displaces a certain volume of water, which is the volume of the submerged portion of the ship.

Suppose you take out the ship and replace the volume of the submerged portion of the ship by water, so that the water level becomes same everywhere. How much does this volume of water weigh? If it weighs, say, more than the ship, then the pressure on A will definitely be more than that at B.

What does your instinct say? And Physics?