Conducting slidewire see system-Faraday's Law

[Gemma95]

Homework Statement

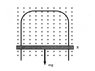
A conducting slidewire system is set up as shown. The sliding wire has mass m and electrical resistance R and falls under gravity as shown. The fixed wire loop has zero resistance and lies perpendicular to a uniform magnetic field B shown pointing into the page.
i) Use Faraday's Law to determine the maximum velocity of the slidewire.
ii) How much power is dissipated at the peak velocity?

Homework Equations

ɛ=-dФ/dt
P=(I^2)R

The Attempt at a Solution

I defined the area vector as pointing in the same direction as the magnetic field, so
ɛ=-B(dA/dt)
In time dt the slidewire moves a distance vdt, giving ɛ=-BLv where L is the width of the slidewire.
I think I am simplifying the problem too much by simply rearranging for v in this equation and obtaining
v=-ɛ/BL -should I differentiate in order to maximise v? I feel I am missing something by not including the given mass m.

For the second part, overall current I=|ɛ|/R, so I=BLv/R
P=I^2R=(BLv/R)^2/R

P(dissipated)=(B^2L^2v^2)/R

Thanks in advance for any help, much appreciated.

 

[BvU]

But with v=-ɛ/BL you haven't determined v yet, have you !?

Is there something that stops you from answering e.g. $v = -{\tfrac 1 2} g t^2$ ?

[edit]

Thanks in advance for any help, much appreciated

Not so certain my help has helped. Can you enlighten me ?