christof6869
- 5
- 0
Homework Statement
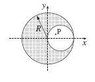
The conductor is cylindrically shaped with a radius of R. The hole on the inside is also cylindrically shaped with a radius of R/2. If a cross-section of this conductor is placed on an x-y coordinate plane, the hole would be centered on the x-axis at a distance of R/2 from the origin. See the attached figure. There is a current going through the conductor "out of the screen" or toward us, given as I, and it is uniformly distributed throughout the filled region. I need to find the magnetic field at any arbitrary point P inside the cavity.
Homework Equations
I know that this is an ampere's law problem similar to finding the magnetic field inside a cylindrical wire. You consider the radius of the closed loop to be less than the outer radius of the wire and, since the current is uniform, the field ends up being equivalent to the permeability of free space constant times the current enclosed multiplied by the ratio of areas.
B=mu0I x (r2/R2)
The Attempt at a Solution
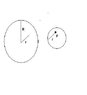
I tried to go about this by imagining the wire to be a combination of two wires, where wire 1 is a larger, circular wire with the current I and the smaller circular wire has the same current in the opposite direction. By combining the two you get a hole with no current of the desired geometry. See Figure 2.
For the larger wire, a smaller radius r is used, this allows us to find the magnetic field due to the filled region of a radius r centered at the origin. I know it will be tangential to the loop I chose and that the result is going to be the same as the one in the given equations.
For the smaller wire, the loop is going to be arcing through the cross section at some arbitrary distance equivalent to r. If I convert this to polar coordinates, the area is pretty easy to find.
x=cos(theta)
y=sin(theta)
r=x2+y2
The wire can be represented by the polar equation for a circle centered on the x-axis with radius R/2.
r1 = 2(R/2)cos(theta) = Rcos(theta)
and the loop "arcing" through the circle is simply a circle, so...
r2= r
Now here's where things get sticky. In order to set up the area integral, I need to find the limits. I think I can do this by setting r1 and r2 equal to each other.
Rcos(theta) = r
cos(theta) = r/R
I want an arc who's cosine ratio is r/R and there are two angles that are equal and opposite, but I don't know how to represent them as two definite limits. This is the problem I'm having.
Once I do that integral, I'll be able to use superposition of the two tangential vectors for magnetic field lines at any arbitrary point by subtracting the magnetic field of wire 2 from wire 1.
B = B1 - B2
= mu0 (Ienclosed_1 - Ienclosed_2)
= mu0 (I x (r2/R2) - Ienclosed_2)
And that should give me what I need. Since the current is uniform throughout, I'm able to do it this way. If it wasn't I believe I would need a more general way of doing it.
Attachments
Last edited: