Enelafoxa
- 12
- 2
Homework Statement
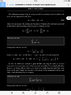
Use the diffence method to sum the series ##\sum_{n=2}^N\frac {2n-1}{2n^2(n-1)^2}##
Homework Equations
from the textbook by Riley i have ##S_N=\sum_{k=1}^m f(N-k+1)-\sum_{k=1}^m f(1-k)##
The Attempt at a Solution
I prefer to write it as ##S_N=\sum_{k=1}^m f(N-m+k)-\sum_{k=1}^m f(k-m)##
And i write the problem as ##S=-\frac1 2 \sum_{n=0}^{N-2} \left(\frac1{(n+2)^2}-\frac1{(n+1)^2}\right)## so we have ##f(n)=-\frac1{2(n+2)^2}## and ##m=1##
##\begin{align}S_N &=\sum_{k=1}^1 f((N-2)-1+k) - \sum_{k=0}^1 f(k-1)\nonumber\\&=f(N-2)-f(0)\nonumber\\&=-\frac1 2\left(\frac 1 {N^2} - \frac 1 {2^2}\right)\nonumber\end{align}## I know this is wrong but why?
But if i write the problem as ##S=-\frac 1 2 \sum_{n=1}^{N-1} \left(\frac1{(n+1)^2}-\frac 1 {n^2}\right)## so that ##f(n)=-\frac 1{2(n+1)^2}## and ##m=1##. Processing as the previous result we get ##S_N=-\frac 1 2\left(\frac 1 {N^2} - 1\right)## and i get the right answer.
My question is why the first way is wrong and the second way is right ( i mean it produce the right answer). I know how to do this problem without using the formula given by the book. I just want to try it with the difference method.
Last edited: