Abdul.119
- 73
- 2
So I was reading a solution of a problem that has to do with integration in polar coordinates, and in one of the steps it did this
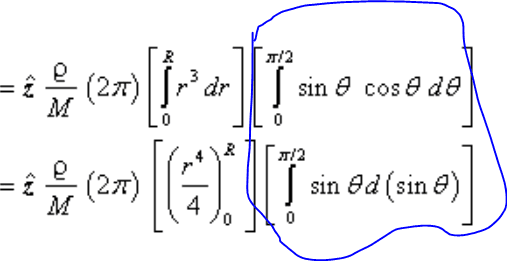
How did these terms (circled in blue) change like that? I've never seen a step like that before..
How did these terms (circled in blue) change like that? I've never seen a step like that before..