Conservation of energy in a circle arc.

[tomkoolen]

http://www.natuurkunde.nl/servlet/supportBinaryFiles?referenceId=1&supportId=606217

Hello everyone,

I was wondering if anyone could shed some light on the following problem:

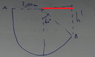
While composing a practise test for a chapter about conservation of energy, I made a problem like the one in the image, but because I was too fast I used physically impossible values: radius = 2.0 m, α = 60° and the friction force equals 10 N. This obviously meant that v^2 gave a negative value.

However that's a problem easily solved by fixing the values. The problem I came across is that I got a different solution than someone else, while the only difference in our calculations was where we put the y = 0 line.

I considered the bottom B of the circle to be y = 0, which means that you get potential energy on the left and the right side of the balance.

The other person put the y = 0 at the horizontal line through C which means that he only gets mgΔy at the left side.

Has anyone got a clue as to why we get different values?

Thanks in advance,
Tom Koolen

 

[TSny]

Either approach will work. Can you state the specific expressions for the initial and final values of y that were used for the two approaches? The difference Δy = y_f-y_i should of course come out the same for the two approaches.

[Note: the assumption of a constant friction force is somewhat unrealistic in this problem since the normal force will vary during the motion. But, as a practice exercise I think it's ok.]

 

[tomkoolen]

Thanks for your response, here are the y-values:

Approach 1: yA = 2.0 meters, yC = 2-2*tan(30) = 0.8 meters
Approach 2: deltay = 1.2 meters and that potential energy is fully converted into friction heat and kinetic energy.

 

[TSny]

I don't think the tangent is the correct trig function to use here.

To see why the two approaches are not yielding the same answers, it would probably be best to post the details of each calculation.

 

[tomkoolen]

Alright, here's the work:

Approach 1: see attachment.
Approach 2:
mgΔy = F*s + 1/2mv^2
35 = 52 + 1.5v^2
v^2 = -11.3

The difference is only 1, but still.
I believe the tangent is correct, but apart from that, it should still give the same answer because both approaches have used the tangent.

Hopefully you can find something in the work!

 

[tomkoolen]

I stand by that last sentence, but I agree that the tangent was incorrect, that was a quick thinking mistake.

 

[TSny]

I have snipped a bit of your picture and attached it here. Note that the red horizontal line is not equal to 2.0 m.

It also appears to me that you have not used the same value of the mass in various parts of your equations. What is the value of the mass?

 

[tomkoolen]

True I see that now, thanks :)
The mass equals 3 kg.