Constrained Lagrangian Problem

[esoms]

Homework Statement

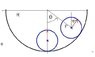
Suppose we have a skateboard half-pipe. The half-pipe has a radius R. We take a bicycle wheel of radius ρ and let it roll into the half-pipe. The wheel rolls without slipping ( and doesn't fall over, of course). Let Θ be the angle from the vertical to the line connecting the center of the half-pipe to the center of the bicycle wheel, and ø the angle the bicycle wheel has rotated.

(a) how are Θ,ø, R and ρ connected if the wheel rotates without slipping?

(b) Find the Lagrangian for the bicycle wheel. Use your answer from the previous part to simplify the Lagrangian.

Homework Equations

L= T-U
where L is the Lagrangian, T is the kinetic engery, and U is the potential energy

The Attempt at a Solution

I am very familiar with how to evaluate and set up lagrangians. However i am having trouble figuring out how to relate the variables for part a. I know the potential will be in the form of U=mgh and how to take partials to get the equations of motion.

It may be that i am confused about the angle Θ and where it is defined. something just isn't clicking. Any point in the right direction would be greatly appreciated. mostly i just need another mind to help me decipher how to do this. Once i get the relationships i should be good to continue on.


Thanks so much for all the help,

Eric

 

[ehild]

Hi Eric, welcome to PF!

Imagine that a line is painted across the wheel, and it is vertical when the wheel is at the bottom of the tube. φ is the angle that line encloses with the vertical as shown in the figure, and θ is the angle showing the position of the centre of the wheel with respect to the vertical.

The wheel spins around its axis, and the centre of the wheel moves along a circle around the centre of the tube.

ehild