MMCS
- 151
- 0
This problem has a lot of calculations from the beginning so i have skipped to the part i am stuck with and tried to include relevant information, apologies if i have missed anything. Assume all working is correct as i was given the answers.
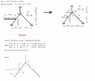
After carrying out the stiffness matrix method I am trying to construct a bending moment diagram using member equilibrium, see attached.
The specific problem is member 1-5
working
member 1-4
bending moment at 1 (given) 123.33Kn
vertical force 57.44Kn
length 2.5
therefore
123.33 - 57.44Kn*2.5 = -20.27 (correct)
Member 4 -5
-20.67 + 160KN(moment from pre-eliminated beam) = 139.63Kn (correct)
however i can not get the moment of -123.98 at point 5
attempt member 4-5
vertical force relative to beam = 80 (sin(36.87)
moment = 139.63Kn
139.63Kn - 80 sin(36.87)*2.5 = 19.629 (incorrect)
After carrying out the stiffness matrix method I am trying to construct a bending moment diagram using member equilibrium, see attached.
The specific problem is member 1-5
working
member 1-4
bending moment at 1 (given) 123.33Kn
vertical force 57.44Kn
length 2.5
therefore
123.33 - 57.44Kn*2.5 = -20.27 (correct)
Member 4 -5
-20.67 + 160KN(moment from pre-eliminated beam) = 139.63Kn (correct)
however i can not get the moment of -123.98 at point 5
attempt member 4-5
vertical force relative to beam = 80 (sin(36.87)
moment = 139.63Kn
139.63Kn - 80 sin(36.87)*2.5 = 19.629 (incorrect)