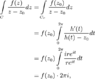You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Contour Integral to Properly Posting Math Problems on Online Forums
- Thread starter Othman0111
- Start date
-
- Tags
- Contour integral Integral
AI Thread Summary
Properly posting math problems on online forums requires typing out the problem statement and any work rather than relying solely on images. Images can be difficult to read and may lead to posts being ignored or deleted due to forum guidelines. Clear, typed submissions facilitate easier responses and engagement from others. When images are necessary, they should be well-focused and attached directly to the post. Adhering to these practices enhances the likelihood of receiving helpful feedback.
Physics news on Phys.org
Othman0111
- 27
- 0
This is my first time here. Please don't delete my thread.
Othman0111
- 27
- 0
The code I tried to input:
In[64]:= r = 2;
i = Sqrt[-1];
x[t_] := r*Cos[t] - 1;
y[t_] := r * Sin[t] - i;
K[x_, y_] := {x + i y}
In[70]:= f[K_] := 1/(K - (1 + i))
In[71]:= Integrate[f[K], {t, 0, 2 \[Pi]}]
Out[71]= (2 \[Pi])/((-1 - I) + K)
the output should be 2πi. Right?
In[64]:= r = 2;
i = Sqrt[-1];
x[t_] := r*Cos[t] - 1;
y[t_] := r * Sin[t] - i;
K[x_, y_] := {x + i y}
In[70]:= f[K_] := 1/(K - (1 + i))
In[71]:= Integrate[f[K], {t, 0, 2 \[Pi]}]
Out[71]= (2 \[Pi])/((-1 - I) + K)
the output should be 2πi. Right?
- 11,326
- 8,750
Your handwritten picture is not readable. You are violating our guidelines.
https://www.physicsforums.com/threads/guidelines-for-students-and-helpers.686781/ said:
- Do not simply post images of the problem statement or your work.
Please make the effort to type up the problem statement and your work. Ask yourself "If I can't be bothered to spend my time typing it, why should they be bothered to spend their time reading it, much less responding to it?" Use images for supporting figures. You may, of course, attach an electronic copy of the problem statement in addition to the typed version. Indeed, if it's a complicated or long problem, you probably should, but you should always provide a typed version as well.
While posting images may be convenient for you, it's actually one of the most effective ways of getting your request for help ignored. Images are often too big, too small, rotated, upside down, out of focus, dimly lit, or of otherwise poor quality. Your handwriting may not be as easy to read as you think it is. Even when images are readable, they often make viewing and responding to a thread very inconvenient, particularly on a mobile device. Moreover, they're a hindrance to the helpers as portions of the problem statement or your work can't easily be quoted. Using images alone doesn't qualify as filling out the homework template, so your post may be deleted.- Don't post poor images.
When you do use an image in your post, make sure it's in focus, oriented the right way, well lit, etc. It seems like this should be obvious, but experience has shown that people frequently post incredibly poor images. Add images as attachments to the post. Don't host it externally. That way it will remain on PF indefinitely, and your thread will remain useful to future visitors.
In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question.
Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point?
Lets call the point which connects the string and rod as P.
Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
This problem is two parts. The first is to determine what effects are being provided by each of the elements - 1) the window panes; 2) the asphalt surface. My answer to that is
The second part of the problem is exactly why you get this affect.
And one more spoiler:
Let's declare that for the cylinder,
mass = M = 10 kg
Radius = R = 4 m
For the wall and the floor,
Friction coeff = ##\mu## = 0.5
For the hanging mass,
mass = m = 11 kg
First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on.
Force on the hanging mass
$$mg - T = ma$$
Force(Cylinder) on y
$$N_f + f_w - Mg = 0$$
Force(Cylinder) on x
$$T + f_f - N_w = Ma$$
There's also...
Similar threads
- Replies
- 1
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 1
- Views
- 2K
- Replies
- 38
- Views
- 7K
- Replies
- 5
- Views
- 3K
- Replies
- 2
- Views
- 894
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 5
- Views
- 652
- Replies
- 2
- Views
- 1K
Hot Threads
-
The problem of one tube and two balls on a plane
- Started by crazy lee
- Replies: 60
- Introductory Physics Homework Help
-
Collision of a bullet on a rod-string system: query
- Started by palaphys
- Replies: 70
- Introductory Physics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 0
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 78
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math