You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Control design for PWM converter
AI Thread Summary
Hubert is seeking assistance with his PWM converter design, specifically regarding the integration of an INA210 for feedback and the implementation of temperature monitoring for an LED to prevent overheating. He discusses the challenges of maintaining high efficiency while incorporating a potentiometer and considers using an LM335 IC temperature sensor or thermistor for temperature measurement. Baluncore provides insights on modeling the LED's behavior and suggests using LM334 current sources to manage LED current based on temperature. The conversation emphasizes the importance of calibration and adjusting circuit components to ensure effective thermal management and efficiency in the design.
Engineering news on Phys.org
Svein
Science Advisor
- 2,316
- 813
The main difference is the removal of the reference voltage.
If VLED<1.5V, no current flows through the LED, the output of the INA210 is 0V - and that is what you use as a reference voltage.
If VLED<1.5V, no current flows through the LED, the output of the INA210 is 0V - and that is what you use as a reference voltage.
Hubert Tchio
- 38
- 0
Hi Svein,
thanks for your fast reply, so how can i add the INA210 in my circuit into for the circuit to be functional as required?
thanks for your fast reply, so how can i add the INA210 in my circuit into for the circuit to be functional as required?
Svein
Science Advisor
- 2,316
- 813
Start with your first circuit. This has VLED as a feedback - when it increases, it is regulated down. If you look at the output of INA210, you have the same polarity - when the output increases, you want VLED to go down. Thus - sum VLED and the output of INA210 using a resistor in series with each. Experiment with the relation between the resistors. Or - insert a 10k potentiometer with VLED and the output of INA210 at each end and the slider to the op-amp input.
Hubert Tchio
- 38
- 0
Hi Svein, thank but i don't get it.
please can you just give me a rough sketch of what you mean?
please can you just give me a rough sketch of what you mean?
Svein
Science Advisor
- 2,316
- 813
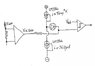
Like this. Use your first circuit, add the INA210 and connect the output as shown here.
Hubert Tchio
- 38
- 0
Hi Svein,
thank you for your response, but i believe adding a 10K in the circuit also increase power loss thereby reducing the overall efficiency of my design (correct me if I am wrong).
I wish to have a design with high efficiency.
thank you for your response, but i believe adding a 10K in the circuit also increase power loss thereby reducing the overall efficiency of my design (correct me if I am wrong).
I wish to have a design with high efficiency.
Svein
Science Advisor
- 2,316
- 813
Hubert Tchio said:thank you for your response, but i believe adding a 10K in the circuit also increase power loss thereby reducing the overall efficiency of my design (correct me if I am wrong).
- The regulator system tends to minimize the voltage across the potentiometer.
- Even with a voltage of 1V across the potentiometer, the current through it is negligible compared to the power draw of the rest of your circuit.
Hubert Tchio
- 38
- 0
Hi Svein,
Thanks. I will look at the document and get back to you.
Best regards
Hubert
Thanks. I will look at the document and get back to you.
Best regards
Hubert
Hubert Tchio
- 38
- 0
@Svein,
thank you so much, your idea works perfectly and the problem is solved.
My second problem is still without a solution. Can anyone help?
how to use another current monitor to measure the LED current and use it as feedback to the temperature measurement? The Goal is to fix a maximum temperature for the LED.
Best regards
Hubert
thank you so much, your idea works perfectly and the problem is solved.
My second problem is still without a solution. Can anyone help?
how to use another current monitor to measure the LED current and use it as feedback to the temperature measurement? The Goal is to fix a maximum temperature for the LED.
Best regards
Hubert
Baluncore
Science Advisor
- 16,483
- 10,188
As I understand it, you intend to use the LED current and LED forward voltage to identify the LED die temperature.Hubert Tchio; in .pdf said:Secondly, I indeed to add a temperature measurement as an additional input but I don’t know how to do this. What I mean is to put another current monitor to measure the LED current and use it as feedback to the temperature measurement. I don’t intern to use a temperature sensor.
Can anyone be of help?
Will you then back-off the current to limit LED temperature rise?
What make and model LED are you using?
Can you please post your latest schematic model.
Hubert Tchio
- 38
- 0
Hi Baluncore,
Thank you once more for your time.
Yes you understood what my plans are. Indeed, i will then back off the current to limit LED temperature rise.
I am using an OSRAM LUW HWQP LED "3.25V and 1A "
Here attached is my lastest schematic. I can also feed VLED directly to the Error amp. Vref is my precison output voltage.
Thanks in Advance.
Best regards
Hubert
Thank you once more for your time.
Yes you understood what my plans are. Indeed, i will then back off the current to limit LED temperature rise.
I am using an OSRAM LUW HWQP LED "3.25V and 1A "
Here attached is my lastest schematic. I can also feed VLED directly to the Error amp. Vref is my precison output voltage.
Thanks in Advance.
Best regards
Hubert
Attachments
Baluncore
Science Advisor
- 16,483
- 10,188
Re: OSRAM LUW HWQP data sheet;
http://www.osram-os.com/Graphics/XPic4/00151034_0.pdf/LUW HWQP - OSLON Black Flat.pdf
With Ifwd = 1A and Vfwd = 3.35V the LED will have 3.35 W power dissipation.
Knowing from the table on page 4 that the thermal resistance is 5.5°C / W.
We can expect a temperature rise of 5.5°C * 3.35W = 18.5°C
To limit junction temperature to 125°C requires the environment remain below about 105°C.
Relative Forward Voltage versus temperature is shown at the top left of page 10.
It shows that relative to 25°C, at the maximum operating temperature of 125°C, the voltage will have fallen by only 0.18V
This is less than the manufacturing tolerance grades, 8F, 8G & 8H listed at the bottom of page 5.
The Characteristics table on page 4, shows a 0.75 volt manufacturing spread.
It will therefore not be possible to determine temperature from Vfwd without a calibration process.
You will probably need to calibrate every LED with short "on" pulses to measure Vfwd at 25°C.Relative spectral emission, at the top of page 8, shows a peak at 440nm in the blue.
Knowing that " Energy = Plank's constant * frequency " we can compute Vfwd = 1240 / 440nm = 2.818V.
Ignoring the Gaussian thermal energy spreading expected, that should be the intercept of the Ifwd curve with Vfwd axis.
Looking at the graph of Ifwd versus Vfwd, (top left of page 9), we see it passes through the point 3.4V at 1.4A
The series resistance of the LED will be Rs = (3.4V - 2.818V) / 1.4A = 0.416 ohms
We can predict Vfwd at Ifwd = 1A as being 2.818V + ( 1.0A * 0.416R) = 3.234
The graph shows that it is a close enough model.
So the LED can be modeled as a 1.818V bandgap in series with a series resistor of about 0.416 ohms.
http://www.osram-os.com/Graphics/XPic4/00151034_0.pdf/LUW HWQP - OSLON Black Flat.pdf
With Ifwd = 1A and Vfwd = 3.35V the LED will have 3.35 W power dissipation.
Knowing from the table on page 4 that the thermal resistance is 5.5°C / W.
We can expect a temperature rise of 5.5°C * 3.35W = 18.5°C
To limit junction temperature to 125°C requires the environment remain below about 105°C.
Relative Forward Voltage versus temperature is shown at the top left of page 10.
It shows that relative to 25°C, at the maximum operating temperature of 125°C, the voltage will have fallen by only 0.18V
This is less than the manufacturing tolerance grades, 8F, 8G & 8H listed at the bottom of page 5.
The Characteristics table on page 4, shows a 0.75 volt manufacturing spread.
It will therefore not be possible to determine temperature from Vfwd without a calibration process.
You will probably need to calibrate every LED with short "on" pulses to measure Vfwd at 25°C.Relative spectral emission, at the top of page 8, shows a peak at 440nm in the blue.
Knowing that " Energy = Plank's constant * frequency " we can compute Vfwd = 1240 / 440nm = 2.818V.
Ignoring the Gaussian thermal energy spreading expected, that should be the intercept of the Ifwd curve with Vfwd axis.
Looking at the graph of Ifwd versus Vfwd, (top left of page 9), we see it passes through the point 3.4V at 1.4A
The series resistance of the LED will be Rs = (3.4V - 2.818V) / 1.4A = 0.416 ohms
We can predict Vfwd at Ifwd = 1A as being 2.818V + ( 1.0A * 0.416R) = 3.234
The graph shows that it is a close enough model.
So the LED can be modeled as a 1.818V bandgap in series with a series resistor of about 0.416 ohms.
Hubert Tchio
- 38
- 0
Hi Baluncore,
Thank you for your time and effort put together to help me. But I must admit, i do not get it.
Are you saying my actual schematic is enough? should I just change the series Resitor to 0.416 ohms and the work is done?
Or is there anything to do next?
Best regards
Hubert
Thank you for your time and effort put together to help me. But I must admit, i do not get it.
Are you saying my actual schematic is enough? should I just change the series Resitor to 0.416 ohms and the work is done?
Or is there anything to do next?
Best regards
Hubert
Baluncore
Science Advisor
- 16,483
- 10,188
No.A model of the LED you are using looks like a voltage step in series with a resistor having a value of about 0.416 ohms.Hubert Tchio said:Are you saying my actual schematic is enough? should I just change the series Resitor to 0.416 ohms and the work is done?
I am saying that it will be very difficult for you to implement LED die temperature estimation by monitoring LED Vfwd and Ifwd.
I would not take it on without a micro-controller to first calibrate the LED model and then monitor the model on the fly.
Hubert Tchio
- 38
- 0
Hi Baluncore,
thanks for your reply. Permit me to ask a foolish way. Do you think there is any other way to implement LED die temperature on the model of the LED i am using?
I am still trying to figure that out.
Thanks in advance
thanks for your reply. Permit me to ask a foolish way. Do you think there is any other way to implement LED die temperature on the model of the LED i am using?
I am still trying to figure that out.
Thanks in advance
Baluncore
Science Advisor
- 16,483
- 10,188
Baluncore said:To limit junction temperature to 125°C requires the environment remain below about 105°C.
By independently monitoring LED heatsink or substrate temperature, you can reduce the duty cycle, the LED current and so LED power dissipation as the environmental temperature approaches the limit of 105°C. If the change begins only at 95°C and takes place so that current falls linearly to zero at 105°C, then the LED will be over-temperature protected. That might be achieved by reducing the current reference voltage at high temperatures.Hubert Tchio said:Do you think there is any other way to implement LED die temperature on the model of the LED i am using?
Baluncore
Science Advisor
- 16,483
- 10,188
@ Hubert Tchio. Looking at your circuit diagram, you have X2, a high-side P-channel MOSFET switch. N-channel MOSFETS have lower on-resistance, less drive requirements and switch faster for the same price. I believe you should invert your design to use the lower cost and more efficient switch.
You drive the gate of X2 with a voltage comparator, U39, hopefully it has some feed-forward to speed up the transition. But does it have the drive needed, (about 100mA), to switch X2 quickly through the inefficient transition?
You drive the gate of X2 with a voltage comparator, U39, hopefully it has some feed-forward to speed up the transition. But does it have the drive needed, (about 100mA), to switch X2 quickly through the inefficient transition?
Hubert Tchio
- 38
- 0
@Baluncore . Thanks for your feedback. I will try the circuit with a high-side N-channel MOSFET switch to see what i get.
So far the ciruit is ok. The voltage comparator compares my control voltage and my ramp input to provide a PWM signal at the output for driving the X2.
My main problem now is still on how to implement a temperature measurement. I have decided to go for an LM335 IC temperature sensor or themistor, I have built a thermal design, it seems ok but I still don't know how to integrate this thermal design to my current LED driver. It would have been easy if my thermal design switches off (input to ground) my LED driver when the temperature is too high but rather the thermal design should reduce the forward current instead.
Still looking for help.
Best regards
Hubert
So far the ciruit is ok. The voltage comparator compares my control voltage and my ramp input to provide a PWM signal at the output for driving the X2.
My main problem now is still on how to implement a temperature measurement. I have decided to go for an LM335 IC temperature sensor or themistor, I have built a thermal design, it seems ok but I still don't know how to integrate this thermal design to my current LED driver. It would have been easy if my thermal design switches off (input to ground) my LED driver when the temperature is too high but rather the thermal design should reduce the forward current instead.
Still looking for help.
Best regards
Hubert
Baluncore
Science Advisor
- 16,483
- 10,188
To taper the LED current from a maximum at 95°C to zero at 105°C you can use a couple of LM334 Current Sources. They are available in 3 terminal TO-92 package. Get the data sheet from; http://www.ti.com/general/docs/lit/getliterature.tsp?genericPartNumber=lm334&fileType=pdf
Set up two in series, between the supply rails. (See the attached sketch). One configured as a temperature sensor, see page 6, fig 13; set it to 1uA per °K. The other as a zero tempco source, see page 8, fig 15; set it to (95°C+273°K) = 368uA.
Now place the two together in thermal contact with the LED mounting. A difference current is available at the junction node of the two. Take that current through a signal diode to a resistor connected to the current sensor output. Once the temperature reaches 95°C the diode will conduct and add voltage to the current sense voltage. The current will be reduced as a result. Select the resistor to give zero LED current when 10uA flows. For 1A LED current, (giving a 2 volt signal), use R = 2V / 10uA = 200k.
Set up two in series, between the supply rails. (See the attached sketch). One configured as a temperature sensor, see page 6, fig 13; set it to 1uA per °K. The other as a zero tempco source, see page 8, fig 15; set it to (95°C+273°K) = 368uA.
Now place the two together in thermal contact with the LED mounting. A difference current is available at the junction node of the two. Take that current through a signal diode to a resistor connected to the current sensor output. Once the temperature reaches 95°C the diode will conduct and add voltage to the current sense voltage. The current will be reduced as a result. Select the resistor to give zero LED current when 10uA flows. For 1A LED current, (giving a 2 volt signal), use R = 2V / 10uA = 200k.
Attachments
Hubert Tchio
- 38
- 0
Hi Baluncore,
thank you very much, i haven't had time to look at it. I will do that very soon and get back to you.
Once more thank you.
Best regards
Hubert
thank you very much, i haven't had time to look at it. I will do that very soon and get back to you.
Once more thank you.
Best regards
Hubert
Hubert Tchio
- 38
- 0
@Baluncore,
here is Hubert again. I just want to make sure i undesrtood your last mail. Please when you have time can you go through the attached documents?
I will be waiting for your feedback.
Have a great day!
Best regards
Hubert
here is Hubert again. I just want to make sure i undesrtood your last mail. Please when you have time can you go through the attached documents?
I will be waiting for your feedback.
Have a great day!
Best regards
Hubert
Attachments
Baluncore
Science Advisor
- 16,483
- 10,188
You seem to have understood the concept. Now just to fix the numbers.
The LM334 temp sensor setting resistor is usually specified as 226 ohms for 1uA / °K. I don't follow your 83.4K.
At 25°C = 298°K, the reference voltage of the LM334 is effectively 67.7mV.
For 1uA / °K, R = 67.7mV / 298uA = 227 ohms.
The two LM334s and the zero tempco diode should all be kept at the LED heatsink temperature, calibration then only requires adjustment of the temp sensor resistor to match the reference current at 95°C. The choice of 1uA / °K is arbitrary, but is probably sufficient.
A temperature of 10°C over the balance point at 95°C must fake the equivalent of 1A LED current. The INA210 has a gain of 200. If your LED current sense resistor is still 0R025 then 1A will give 0.025 * 200 = 5.0V which is too close to the rails. I would make it closer to 2.5V where the LM334s will be balanced when needed. You need to halve the sense resistor or change to the INA214 which has a gain of 100. Anyhow, back to the value of R. 10uA must drop 2.5V so R = 2.5 / 10uA = 250k.
The LM334 temp sensor setting resistor is usually specified as 226 ohms for 1uA / °K. I don't follow your 83.4K.
At 25°C = 298°K, the reference voltage of the LM334 is effectively 67.7mV.
For 1uA / °K, R = 67.7mV / 298uA = 227 ohms.
The two LM334s and the zero tempco diode should all be kept at the LED heatsink temperature, calibration then only requires adjustment of the temp sensor resistor to match the reference current at 95°C. The choice of 1uA / °K is arbitrary, but is probably sufficient.
A temperature of 10°C over the balance point at 95°C must fake the equivalent of 1A LED current. The INA210 has a gain of 200. If your LED current sense resistor is still 0R025 then 1A will give 0.025 * 200 = 5.0V which is too close to the rails. I would make it closer to 2.5V where the LM334s will be balanced when needed. You need to halve the sense resistor or change to the INA214 which has a gain of 100. Anyhow, back to the value of R. 10uA must drop 2.5V so R = 2.5 / 10uA = 250k.
Hubert Tchio
- 38
- 0
@Baluncore
Thank you so much, here is an update.
I hope i get it this time around. Have a great evening.
Best regards
Hubert
Thank you so much, here is an update.
I hope i get it this time around. Have a great evening.
Best regards
Hubert
Attachments
Baluncore
Science Advisor
- 16,483
- 10,188
(A). You need the current summing node of the circuit to be away from the supply rails so as to give the LM334 some operating voltage. That is why I suggest 2.5V. The lower LM334 is in series with a diode so it requires about 1.5V to operate. The current summing diode gives a little more headroom by moving the voltage of the summing node up. Maybe use two or three signal diodes in series to raise the LM334 voltage? The current summing node is only important while operating in balance. Your Rsense 0R004 is a very low resistance to use as a shunt. It will need to be an expensive 4 terminal resistor so as to separate the effects of resistance in the main current terminals. You could make your own 0R004 by soldering two voltage taps onto a shunt wire. I would use Rsense = 0R0125.
(B). That is better, but you will adjust the value to trim the system to cut-off at 105°C once it is built.
( C). Close enough. Any variation in the individual circuit will be canceled by the adjustment as in (B). It does not really matter if ILED cuts off over a range of 5°C or 15°C, so long as the final shut-down occurs at or below 105°C.
(D). Correct logic, questionable current summing reference voltage.
(E). Summing up the current difference.
You have drawn your “two terminal zero tempco circuit” upside down.
I would use 1N4148 signal diodes. 1N4001 power diodes are not a good choice for either diode in that circuit as it may have a few uA of temperature variable leakage and a lower forward voltage. Also ask yourself why the ti datasheet shows a 1N457 signal diode in the zero tempco circuit example. You need to use a diode with low reverse leakage for the 95°C current polarity switch, it will be in a regulated temperature environment.
(B). That is better, but you will adjust the value to trim the system to cut-off at 105°C once it is built.
( C). Close enough. Any variation in the individual circuit will be canceled by the adjustment as in (B). It does not really matter if ILED cuts off over a range of 5°C or 15°C, so long as the final shut-down occurs at or below 105°C.
(D). Correct logic, questionable current summing reference voltage.
(E). Summing up the current difference.
You have drawn your “two terminal zero tempco circuit” upside down.
I would use 1N4148 signal diodes. 1N4001 power diodes are not a good choice for either diode in that circuit as it may have a few uA of temperature variable leakage and a lower forward voltage. Also ask yourself why the ti datasheet shows a 1N457 signal diode in the zero tempco circuit example. You need to use a diode with low reverse leakage for the 95°C current polarity switch, it will be in a regulated temperature environment.
Hubert Tchio
- 38
- 0
@Baluncore
I am completely confused. I don't get a bit of it anymore.
I started my design with 0R0250 but was not working until I had to regulate Rsense to 4m ohm. I have tried to change Rsense to 0R0125 or more but my signals are unstable.
I don't undestand what type of current summing node you mean.
here attached is my design, i don't know you can if you can do something on it.
The thermal design is not working.
Thanks in advance
Hubert
I am completely confused. I don't get a bit of it anymore.
I started my design with 0R0250 but was not working until I had to regulate Rsense to 4m ohm. I have tried to change Rsense to 0R0125 or more but my signals are unstable.
I don't undestand what type of current summing node you mean.
here attached is my design, i don't know you can if you can do something on it.
The thermal design is not working.
Thanks in advance
Hubert
Attachments
Baluncore
Science Advisor
- 16,483
- 10,188
What are manufacturer and part numbers for U61, U62, X2, D1, D2 ?
What is frequency, amplitude and offset of the “Triangle” input to U62 ?
What is frequency, amplitude and offset of the “Triangle” input to U62 ?
Hubert Tchio
- 38
- 0
U61 and U61 are LMH6622 from TI
D1 is LUW_HWQP LED from OSRAM
D2 is a normal doide from Pspice
Vramp = 1.8V (3.5V - 1.7V) with 455KHz frequency
D1 is LUW_HWQP LED from OSRAM
D2 is a normal doide from Pspice
Vramp = 1.8V (3.5V - 1.7V) with 455KHz frequency
Hubert Tchio
- 38
- 0
sorry U61 and U62 are the same. Vramp = Triangle
Baluncore
Science Advisor
- 16,483
- 10,188
Attached is the switch, LED current sense and temperature protection sections only. The output will be 2.5V when operating correctly. The LM334 model used has an error, so ignore my resistor value detail in setting my over temperature protection currents.
I will try to get the rest of your circuit into the model later but I'm very busy today.
I will try to get the rest of your circuit into the model later but I'm very busy today.
Attachments
Hubert Tchio
- 38
- 0
@Baluncore,
Thank you so much for your time and the assistance. I am very grateful. I also understand you are very busy.
I will be waiting to hear from you when you are less busy. I will try to simulate this circuit and see the outcome.
Once again thank you.
Best regards
Hubert
Thank you so much for your time and the assistance. I am very grateful. I also understand you are very busy.
I will be waiting to hear from you when you are less busy. I will try to simulate this circuit and see the outcome.
Once again thank you.
Best regards
Hubert
Hubert Tchio
- 38
- 0
@Baluncore
Hope you had a nice weekend, just wish to know if you were able to complete the model as desirer.
Hope you had a nice weekend, just wish to know if you were able to complete the model as desirer.
Baluncore
Science Advisor
- 16,483
- 10,188
@ Hubert.
I have got my spice model of the LM334 operating close enough to the data sheet. We need to have similar models.
What spice model are you using for the LM334 ? Can you please post the text in your LM334.sub file?
I have got my spice model of the LM334 operating close enough to the data sheet. We need to have similar models.
What spice model are you using for the LM334 ? Can you please post the text in your LM334.sub file?
Hubert Tchio
- 38
- 0
@Baluncore
*Selfmade model of the LM334 from National Semiconductor or ST
* Helmut Sennewald
*
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 14
Q1 N003 N003 R 0 npn1 14
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS LM334
*
*Selfmade model of the LM334 from National Semiconductor or ST
* Helmut Sennewald
*
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 14
Q1 N003 N003 R 0 npn1 14
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS LM334
*
Baluncore
Science Advisor
- 16,483
- 10,188
The area parameter of "14" at the end of the Q6 and Q1 lines is wrong. That 14 is from a different ratio parameter specified in the data sheet.Hubert Tchio said:Q6 R N001 v+ 0 pnp1 14
Q1 N003 N003 R 0 npn1 14
You should change the Q6 line to end in an area of 16. You should change the Q1 line to end in an area of 12. The model will then be much more real.
What INA210.sub model do you use ?
Now you can design your temperature compensation circuit. Start here:
1. Make a simple circuit that uses an LM334 that runs on a 2.5V supply. It must source a current of about 1uA per °K. i.e. 273.15uA at 0°C.
You will need to use the .TEMP 0 spice directive while checking current at 0°C, .TEMP 25 at 25°C = 298uA and .TEMP 95 at 95°C = 368uA.
You will only need one resistor, what value does it need to have?
2. Make another LM334 circuit, with a 1N4148 diode, also on 2.5V supply. It should sink a temperature stable current of 368uA at 95°C, i.e. the same as the temp sensor, but it should be reasonably fixed at 368uA across the temperature range. Use the .STEP TEMP 0 100 10 to plot the current, trim the two resistors in the circuit to get the zero tempco. Record the two resistor values.
Let me know when you have those three numbers so I can check your model is working OK.
Hubert Tchio
- 38
- 0
@Baluncore,
ok thank you. I will look at it and get back to you. Thank you for the help so far.
here is the INA210.sub model
* Begin INA210
*****************************************************************************
.SUBCKT INA210 IN+ IN- V+ GND OUT REF
XDP6 GND IN- D_Z26V
XDP5 GND IN+ D_Z26V
R4 INp IN+ 4.9999875K
R3 INm IN- 5.0000125K TC=1.5U
XU1 IN- IN+ GND INp OUT V+ INm INA21Xopa
XDP4 GND REF D_DIS1PN0_52
XDP3 REF V+ D_DIS1PN0_52
XDP2 GND OUT D_DIS1PN0_52
XDP1 OUT V+ D_DIS1PN0_52
R2 REF INp 1.0000025MEG
R1 OUT INm 999.9975K TC=1.5U
.ENDS
*
ok thank you. I will look at it and get back to you. Thank you for the help so far.
here is the INA210.sub model
* Begin INA210
*****************************************************************************
.SUBCKT INA210 IN+ IN- V+ GND OUT REF
XDP6 GND IN- D_Z26V
XDP5 GND IN+ D_Z26V
R4 INp IN+ 4.9999875K
R3 INm IN- 5.0000125K TC=1.5U
XU1 IN- IN+ GND INp OUT V+ INm INA21Xopa
XDP4 GND REF D_DIS1PN0_52
XDP3 REF V+ D_DIS1PN0_52
XDP2 GND OUT D_DIS1PN0_52
XDP1 OUT V+ D_DIS1PN0_52
R2 REF INp 1.0000025MEG
R1 OUT INm 999.9975K TC=1.5U
.ENDS
*
Hubert Tchio
- 38
- 0
@Baluncore
here are my results:
A)Temperature sensor
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
B) Tempco current source
Vsupply(V) R1(ohm) R2(ohm)Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
here are my results:
A)Temperature sensor
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
B) Tempco current source
Vsupply(V) R1(ohm) R2(ohm)Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
Hubert Tchio
- 38
- 0
@Baluncore
sorry about that, here are the correct results
here are my results:
A)Temperature sensor
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
B) Tempco current source
Vsupply(V) R1(ohm) R2(ohm) Iset (uA) temp (degree)
2,5 380 3800 359,81 25
2,5 380 3800 368,25 95
2,5 380 3800 368,74 100
2,5 380 3800 371,58 125
sorry about that, here are the correct results
here are my results:
A)Temperature sensor
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 321,438 25
2,5 226 396,95 95
B) Tempco current source
Vsupply(V) R1(ohm) R2(ohm) Iset (uA) temp (degree)
2,5 380 3800 359,81 25
2,5 380 3800 368,25 95
2,5 380 3800 368,74 100
2,5 380 3800 371,58 125
Baluncore
Science Advisor
- 16,483
- 10,188
Re: (A)Temperature sensor.
For 1uA / 1°K I would expect a current of about 273.15uA at 0°C, you give it as zero.
321.438uA at 25°C ? should that not be about 273°K + 25°C = 298.15uA
396,95uA at 95°C ? should that not be about 273°K + 95°C = 368.15uA
I think you are not using the right transistor areas in your LM334 model.
Please post the LM334.sub model you are now using.
Re: (B)Zero TempCo sink.
I know that R2 should be a little less than 10 * R1. You have not modeled the zero tempco circuit and trimmed it to zero tempco by adjusting R1 & R2.
But first let's fix the LM334.sub model (A)Temperature sensor.
For 1uA / 1°K I would expect a current of about 273.15uA at 0°C, you give it as zero.
321.438uA at 25°C ? should that not be about 273°K + 25°C = 298.15uA
396,95uA at 95°C ? should that not be about 273°K + 95°C = 368.15uA
I think you are not using the right transistor areas in your LM334 model.
Please post the LM334.sub model you are now using.
Re: (B)Zero TempCo sink.
I know that R2 should be a little less than 10 * R1. You have not modeled the zero tempco circuit and trimmed it to zero tempco by adjusting R1 & R2.
But first let's fix the LM334.sub model (A)Temperature sensor.
Hubert Tchio
- 38
- 0
@Baluncore
I tried to change the model as you required
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 16
Q1 N003 N003 R 0 npn1 12
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS LM334
but got these values
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 300,427 25
2,5 226 370,963 95
2,5 226 376,053 100
therefore i kept my settings for the previous measurement
Q6 R N001 v+ 0 pnp1 14
Q1 N003 N003 R 0 npn1 14
I tried to change the model as you required
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 16
Q1 N003 N003 R 0 npn1 12
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS LM334
but got these values
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2,50 226 0 0
2,5 226 300,427 25
2,5 226 370,963 95
2,5 226 376,053 100
therefore i kept my settings for the previous measurement
Q6 R N001 v+ 0 pnp1 14
Q1 N003 N003 R 0 npn1 14
Hubert Tchio
- 38
- 0
@Baluncore
may be i got it this time around
temperature sensor
some modification
Q6 R N001 v+ 0 pnp1 10.36
Q1 N003 N003 R 0 npn1 11
results
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2.50 226 0 0
2,5 226 298.168 25
2,5 226 368.249 95
2,5 226 373.196 100
may be i got it this time around
temperature sensor
some modification
Q6 R N001 v+ 0 pnp1 10.36
Q1 N003 N003 R 0 npn1 11
results
Vsupply(V) Rset(ohm) Iset (uA) temp (degree)
2.50 226 0 0
2,5 226 298.168 25
2,5 226 368.249 95
2,5 226 373.196 100
Hubert Tchio
- 38
- 0
@Baluncore,
here is an update for the Tempco current source for same model
Vsupply(V) R1 R2 Iset (uA) temp (degree)
2,50380 3.35k 0 0
2,5 380 3.35k 369.843 25
2,5 380 3.35k 368.361 95
2,5 380 3.35k 368.164 100
will be grateful to hear from you.
here is an update for the Tempco current source for same model
Vsupply(V) R1 R2 Iset (uA) temp (degree)
2,50380 3.35k 0 0
2,5 380 3.35k 369.843 25
2,5 380 3.35k 368.361 95
2,5 380 3.35k 368.164 100
will be grateful to hear from you.
Baluncore
Science Advisor
- 16,483
- 10,188
The model you started with was the original written by Helmut Sennewald and posted on July 11th 2009. It became widespread because it was discussed in the open forums. The area of transistors Q1 and Q6 were both then set at 14, but that 14 in the data sheet is not actually the transistor area, it is a minimum specification for the ratio of Iset to Ibias.
Eventually the model was modified to fix the transistor area bug and posted on April 7th 2011, in the file archive of the yahoo group “LTspice”. (Hidden from google, you need to be a member), https://groups.yahoo.com/neo/groups/LTspice/search/files?query=LM334
LM334.sub 1KB Transistor size changed from 14-14 to 16-12 helmutsennewald Apr 7, 2011
This is now the current version of the LM134 / LM334.sub
* Selfmade model of the LM334 from National Semiconductor or ST
* Helmut Sennewald
*
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 16
Q1 N003 N003 R 0 npn1 12
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1µ
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS
I had reality calibration problems with Helmut Sennewald's old 14-14 model for the LM134 / LM334. When I looked at the LM334 internal design I noticed that the area of Q6 determined the ratio of Iset to IQ2e, a ratio specified in the datasheet to be about 18. Then I needed to select a Q1 area to bring Iset close to the ideal 273.15uA with an Rset of 226 ohms, at a temp= 0°C to get 1uA / 1°K. I ended up with transistor areas of 15.75 and 11.75. Although by using areas of 15.75 and 11.75 it was possible to get a close to perfect 1uA / 1°K model with an Rset of 226 ohms, that was un-real because the 226 ohm resistor specified in the circuits was chosen from the real world E96 standard series of resistor values which has {…, 221, 226, 232, …}, not as the ideal value the circuit needs for Iset = 273.15uA. Also, the area of the transistors should be integer because the transistor mask pattern was originally simply duplicated to make several transistors in parallel. By using areas of 16 and 12 the model was very real and I then needed to find the ideal value of Rset to give 273.15uA at 0°C.
Rset is the magic number you need to find to a couple of decimal places. It is NOT exactly 226.00 ohms.
Once you have found that Rset closest to 226 I will know your model is working and you can then match the I95°C with the zero TempCo current sink.
Note: All this assumes that the NPN1 and PNP1 transistor models being used are realistic. There are also two hidden FETs, Q7 and Q8 being used to start the circuit. They source between 20nA and 200nA. They are not modeled here as the numerical spice model starts OK without them and the start bias currents do not appear to be significant to the model.
Eventually the model was modified to fix the transistor area bug and posted on April 7th 2011, in the file archive of the yahoo group “LTspice”. (Hidden from google, you need to be a member), https://groups.yahoo.com/neo/groups/LTspice/search/files?query=LM334
LM334.sub 1KB Transistor size changed from 14-14 to 16-12 helmutsennewald Apr 7, 2011
This is now the current version of the LM134 / LM334.sub
* Selfmade model of the LM334 from National Semiconductor or ST
* Helmut Sennewald
*
* Pin order: v+ v- R
.SUBCKT LM334 v+ v- R
Q4 N002 N001 v+ 0 pnp1
Q5 N003 N001 v+ 0 pnp1
Q6 R N001 v+ 0 pnp1 16
Q1 N003 N003 R 0 npn1 12
Q2 N002 N003 N004 0 npn1
Q3 N001 N002 R 0 npn1
C1 N002 N004 50p
R2 N004 v- 1µ
R8 v+ v- 1G
C2 v+ v- 10p
C3 N003 v- 1p
C4 R v- 1p
.model npn1 NPN(Is=1e-15 BF=200 TF=1e-9 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.model pnp1 PNP(Is=1e-15 BF=100 TF=1e-7 Cjc=0.5e-12 Cje=1e-12 VAF=100 Rb=100 Re=5)
.ENDS
I had reality calibration problems with Helmut Sennewald's old 14-14 model for the LM134 / LM334. When I looked at the LM334 internal design I noticed that the area of Q6 determined the ratio of Iset to IQ2e, a ratio specified in the datasheet to be about 18. Then I needed to select a Q1 area to bring Iset close to the ideal 273.15uA with an Rset of 226 ohms, at a temp= 0°C to get 1uA / 1°K. I ended up with transistor areas of 15.75 and 11.75. Although by using areas of 15.75 and 11.75 it was possible to get a close to perfect 1uA / 1°K model with an Rset of 226 ohms, that was un-real because the 226 ohm resistor specified in the circuits was chosen from the real world E96 standard series of resistor values which has {…, 221, 226, 232, …}, not as the ideal value the circuit needs for Iset = 273.15uA. Also, the area of the transistors should be integer because the transistor mask pattern was originally simply duplicated to make several transistors in parallel. By using areas of 16 and 12 the model was very real and I then needed to find the ideal value of Rset to give 273.15uA at 0°C.
Rset is the magic number you need to find to a couple of decimal places. It is NOT exactly 226.00 ohms.
Once you have found that Rset closest to 226 I will know your model is working and you can then match the I95°C with the zero TempCo current sink.
Note: All this assumes that the NPN1 and PNP1 transistor models being used are realistic. There are also two hidden FETs, Q7 and Q8 being used to start the circuit. They source between 20nA and 200nA. They are not modeled here as the numerical spice model starts OK without them and the start bias currents do not appear to be significant to the model.
Hubert Tchio
- 38
- 0
@Baluncore
here are today's result for the transistor areas of 10.36 and 11
A) Temp sensor
Rset= 226.03 @25°c, Iset= 298.15uA; @95°c, Iset=368.15uA, @105°c, Iset= 378.16uA
B)
R1= 381.9 ohms and R2 = 3329.3 ohms
@25°c, Iset=370.08uA, @95°c, Iset= 368.15uA @10°C, Iset = 367.71uA
These values change at different room temperature. Yesterday the results for the same settings had some little differences.
Please should we assume these values and proceed to the next level. This is taking too much time.
Thanks for your understanding
Best regards
Hubert
here are today's result for the transistor areas of 10.36 and 11
A) Temp sensor
Rset= 226.03 @25°c, Iset= 298.15uA; @95°c, Iset=368.15uA, @105°c, Iset= 378.16uA
B)
R1= 381.9 ohms and R2 = 3329.3 ohms
@25°c, Iset=370.08uA, @95°c, Iset= 368.15uA @10°C, Iset = 367.71uA
These values change at different room temperature. Yesterday the results for the same settings had some little differences.
Please should we assume these values and proceed to the next level. This is taking too much time.
Thanks for your understanding
Best regards
Hubert
Baluncore
Science Advisor
- 16,483
- 10,188
If you do not use the transistor areas of 12 and 16 then our models will not match and you will not be modelling the LM334.Hubert Tchio said:Please should we assume these values and proceed to the next level. This is taking too much time.
Thanks for your understanding
Your zero TempCo circuit will not work when you build it because of the wrong model ratio of Iset to Ibias.
Hubert Tchio
- 38
- 0
ok, now is done for the transistor areas of 12 and 16
A) Sensor,
Rset = 227.73 ohms and Iset =
@25°C, 298.21uA; @95°C, 368.15uA; @ 105°C, 378.17°C
B)Tempco
R1= 380.29 ohms and R2 = 3313.86 ohms
imply Iset:
@25°C, 368.33uA; @95°C, 368.15uA; @105°C = 368.06uA
A) Sensor,
Rset = 227.73 ohms and Iset =
@25°C, 298.21uA; @95°C, 368.15uA; @ 105°C, 378.17°C
B)Tempco
R1= 380.29 ohms and R2 = 3313.86 ohms
imply Iset:
@25°C, 368.33uA; @95°C, 368.15uA; @105°C = 368.06uA
Baluncore
Science Advisor
- 16,483
- 10,188
That is a nice looking set of numbers now, well done.
See the attached schematic. By connecting the two modules you designed in series, between 0V and +5V, there will be a difference current that is blocked by D1 until the current changes direction and D1 starts to conduct at 95°C. As the temperature rises the difference rises until at 105°C it reaches 10uA. The 10uA will add 2.5V to the output because of R2 = 250k. The 2.5V voltage source, fakes the output from the 1NA210 when ILED = 1A. No LED current is then needed to satisfy the 2.5V input to the controller. The controller will always have an integrator input voltage of 2.5V.
Do you now understand how the difference current works? why it starts at 95°C? and why 250k is used?
The next step is to find an op-amp with low input bias current as your controller integrator and a fast comparator to generate the MOSFET gate drive signal. They need to run on 0V and +5 rails only, which should be no problem, see what you can find, I'll take a look also. The integrator has the 250k input circuit so input bias current must be less than about 100nA, but it does not need to be fast.
See the attached schematic. By connecting the two modules you designed in series, between 0V and +5V, there will be a difference current that is blocked by D1 until the current changes direction and D1 starts to conduct at 95°C. As the temperature rises the difference rises until at 105°C it reaches 10uA. The 10uA will add 2.5V to the output because of R2 = 250k. The 2.5V voltage source, fakes the output from the 1NA210 when ILED = 1A. No LED current is then needed to satisfy the 2.5V input to the controller. The controller will always have an integrator input voltage of 2.5V.
Do you now understand how the difference current works? why it starts at 95°C? and why 250k is used?
The next step is to find an op-amp with low input bias current as your controller integrator and a fast comparator to generate the MOSFET gate drive signal. They need to run on 0V and +5 rails only, which should be no problem, see what you can find, I'll take a look also. The integrator has the 250k input circuit so input bias current must be less than about 100nA, but it does not need to be fast.
Attachments
Hubert Tchio
- 38
- 0
Thank you. I am glad i got some nice values.
I know understand the theory behind it. I must admit i have learned something.
for the integrator op amp:
OPA234 has a bias current of 25nA
LM6132 has a bias current close to 100nA
for a fast comparator:
LMH6622 has a speed of 50MHz, i am targeting 1Mhz switching frequency for the MOSFET
What do you think if I may ask?
I know understand the theory behind it. I must admit i have learned something.
for the integrator op amp:
OPA234 has a bias current of 25nA
LM6132 has a bias current close to 100nA
for a fast comparator:
LMH6622 has a speed of 50MHz, i am targeting 1Mhz switching frequency for the MOSFET
What do you think if I may ask?
Hubert Tchio
- 38
- 0
sorry know=now
Baluncore
Science Advisor
- 16,483
- 10,188
I think you have just demonstrated a fixative attention to detail and the ability to criticize your own language / design. Both those characteristics are essential in competent design engineers. You have realized the importance of understanding what you are trying to do and how you are doing it.Hubert Tchio said:What do you think if I may ask?
It is 6AM here so I will take a look at your component selections later this morning.
Similar threads
- Replies
- 13
- Views
- 6K
- Replies
- 10
- Views
- 2K
- Replies
- 2
- Views
- 2K
- Replies
- 32
- Views
- 5K
- Replies
- 2
- Views
- 2K
- Replies
- 6
- Views
- 959
- Replies
- 1
- Views
- 4K
- Replies
- 9
- Views
- 3K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 3K
Hot Threads
-
How does pulling a string start a lawnmower or a weed eater?
- Started by sevensages
- Replies: 76
- General Engineering
-
Mystery noise in flue (no, it's not a critter)
- Started by DaveC426913
- Replies: 35
- General Engineering
-
Questions about the Tesla turbine
- Started by Chiel555
- Replies: 8
- General Engineering
-
How do wind turbines do their thing?
- Started by DaveC426913
- Replies: 9
- General Engineering
-
Why speed limits don't matter
- Started by 256bits
- Replies: 34
- General Engineering
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 5
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 11
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math