- #1
fab13
- 312
- 6
- TL;DR Summary
- I would like to know the Convention of units for densities in cosmology : I wonder if consistent units are used by multiplying or dividing with Delta_z
I have a table of densities of galaxies :
Expected number density of galaxies for photometric survey per unit area and redshift intervals, ##\mathrm{d} N / \mathrm{d} \Omega \mathrm{d} z\left[\mathrm{sr}^{-1}\right]## and the corresponding density of galaxies per ##\operatorname{arcmin}^2## for each redshift
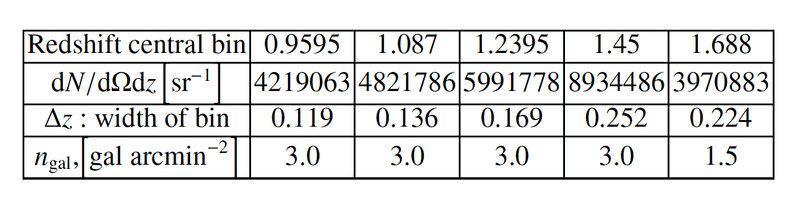
I wonder if the second row values are correct : indeed, I hesitate between both calculus, for example for the bin :
- case 1
3 / 11818102.860 * 0.119 = 4219062.72 (rounded to 4219063) in units ##\text{d}N/\text{d}\Omega\text{d}z##
OR should I set rather :
- case 2
3 / 11818102.860 / 0.119 = 297935366.218 (rounded to 297935366) in units ##\text{d}N/\text{d}\Omega\text{d}z##
One of both is wrong since I don't know if the units are ##\text{d}N/\text{d}\Omega\text{d}z## or ##\text{d}N/\text{d}\Omega/\text{d}z##.
Could anyone help me what is the convention for the units of the writing ##\text{d}N/\text{d}\Omega\text{d}z## that causes some confusions ( we don't know if we have to multiply or divide by ##\Delta z## ?
Expected number density of galaxies for photometric survey per unit area and redshift intervals, ##\mathrm{d} N / \mathrm{d} \Omega \mathrm{d} z\left[\mathrm{sr}^{-1}\right]## and the corresponding density of galaxies per ##\operatorname{arcmin}^2## for each redshift
I wonder if the second row values are correct : indeed, I hesitate between both calculus, for example for the bin :
- case 1
3 / 11818102.860 * 0.119 = 4219062.72 (rounded to 4219063) in units ##\text{d}N/\text{d}\Omega\text{d}z##
OR should I set rather :
- case 2
3 / 11818102.860 / 0.119 = 297935366.218 (rounded to 297935366) in units ##\text{d}N/\text{d}\Omega\text{d}z##
One of both is wrong since I don't know if the units are ##\text{d}N/\text{d}\Omega\text{d}z## or ##\text{d}N/\text{d}\Omega/\text{d}z##.
Could anyone help me what is the convention for the units of the writing ##\text{d}N/\text{d}\Omega\text{d}z## that causes some confusions ( we don't know if we have to multiply or divide by ##\Delta z## ?