Amaelle
- 309
- 54
- Homework Statement
- the convergence of a series (look at the image)
- Relevant Equations
- asymptotic comparison
good day
I want to study the convergence of this serie and want to check my approch
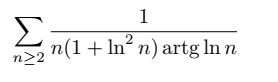
I want to procede by asymptotic comparison
artgln n ≈pi/2
n+n ln^2 n ≈n ln^2 n
and we know that
1/(n ln^2 n ) converge so the initial serie converge
many thanks in advance!
I want to study the convergence of this serie and want to check my approch
I want to procede by asymptotic comparison
artgln n ≈pi/2
n+n ln^2 n ≈n ln^2 n
and we know that
1/(n ln^2 n ) converge so the initial serie converge
many thanks in advance!