Coriolis force and conservation of angular momentum

[Soren4]

I'm trying to understand the relations between the existence of Coriolis force and the conservation of angular momentum. I found this explanation on Morin.

A carousel rotates counterclockwise with constant angular speed ω.Consider someone walking radially inward on the carousel (imagine a radial line painted on the carousel; the person walks along this line), at speed v with respect to the carousel, at radius r. [...]

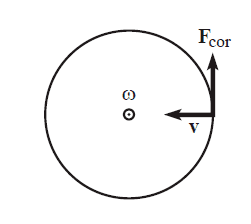
Take d/dt of L = mr^2ω, where ω is the person’s angular speed withrespect to the lab frame, which is also the carousel’s angular speed. Using dr/dt =− v, we have
$$dL/dt =− 2mrωv+mr^2(dω/dt)\tag{1}$$

What if the person doesn’t apply a tangential friction force at his feet? Then the Coriolis force of 2mωv produces a tangential acceleration of 2ωv in the rotating frame, and hence also in the lab frame (initially, before the direction of the motion in the rotating frame has a chance to change), because the frames are related by a constant ω. This acceleration exists essentially to keep the person’s angular momentum (with respect to the lab frame) constant.
[...] To see that this tangential acceleration is consistent with conservation of angular momentum, set dL/dt = 0 in Eq. (1) to obtain 2ωv = r(dω/dt) (this is the person’sω here, which is changing).
The right-hand side of this is by definition the tangential acceleration. Therefore, saying that L is conserved is the same as saying that 2ωv is the tangential acceleration (for this situation where the inward radial speed is v).

I do not understand the two highlighted parts. In particular it seems that Coriolis force is there to change the angular momentum of the person in the lab frame. But this cannot be true since Coriolis force is a fictitious force, existing only in the rotating frame. I don't see clearly the link between Coriolis force and conservation of angular momentum in this case. Can anyone give some further explanations about this?

 

[PeroK]

I'm trying to understand the relations between the existence of Coriolis force and the conservation of angular momentum. I found this explanation on Morin.I do not understand the two highlighted parts. In particular it seems that Coriolis force is there to change the angular momentum of the person in the lab frame. But this cannot be true since Coriolis force is a fictitious force, existing only in the rotating frame. I don't see clearly the link between Coriolis force and conservation of angular momentum in this case. Can anyone give some further explanations about this?

If you are on a spinning carousel and you try to walk towards the centre (using only a force in the radial direction) then the ficticious Coriolis force will knock you off line (as far as the rotating reference frame is concerned). So, in order to walk in a straight line (in the rotating frame) you need to have an additional real tangential force to counteract the Coriolis force. This real tangential force therefore changes your angular momentum.

Note that real and fictitious forces come in pairs that are equal and opposite in an accelerating reference frame:

1) Everything that is accelerating with the frame must have a real force acting on it to maintain the acceleration.

2) Everything that is not constrained to move with the frame has a ficticious force, equal and opposite to the real force, when viewed in the accelerating frame.

So, when you move in a rotating reference frame, there are effectively two Coriolis forces:

1) The real force needed to increase the angular momentum.

2) The fictitious force (equal and opposite to the real one) which explains why you move in a straight line in the rotating frame.

Note that the centripetal/centrifugal force is such a pair - but in this case they are given different names.

Edit: the friction force here is the real opposite of the Coriolis force.

 

[Soren4]

Thanks for your reply! I got your point, but the thing that confuses me is that in this case there is no friction force (nor any other real forces)

What if the person doesn’t apply a tangential friction force at his feet?...

And that's why angular momentum of the person is conserved (no torque exerted on the person).

Nevertheless Coriolis force is present in the rotating frame. I don't understand how Coriolis force is related to the conservation of angular momentum of the person in the lab frame.

In the text it is claimed the existence of a $2v\omega$ tangential acceleration in the lab frame at the beginning. Where does it come from if there is no friction? Immediatley after it says that it's this force the one responsible for conservation of angular momentum. But angular momentum is conserved if no tangential force is applied (i.e. no torque), right? So how can that be possible?

As far as I have understood we have the lab frame (no real forces -> no torque -> angular momentum conserved) and the rotating frame (where there is Coriolis force, and angular momentum is not conserved). But the book says that in some way that conservation of angular momentum and Coriolis effect are related, and I still don't see this relation.

 

[PeroK]

Nevertheless Coriolis force is present in the rotating frame. I don't understand how Coriolis force is related to the conservation of angular momentum of the person in the lab frame.

This has nothing to do with the person in the lab frame. This is all about forces on the person in the rotating frame: either viewed from the rotating frame; or viewed from the lab frame.

Note: I edited my first post as Morin is quite careful to use the Coriolis force as the fictitious force only.

the thing that confuses me is that in this case there is no friction force (nor any other real forces)

And that's why angular momentum of the person is conserved (no torque exerted on the person).

As far as I have understood we have the lab frame (no real forces -> no torque -> angular momentum conserved) and the rotating frame (where there is Coriolis force, and angular momentum is not conserved). But the book says that in some way that conservation of angular momentum and Coriolis effect are related, and I still don't see this relation.

It's difficult to answer so many questions. In general, you seem to try to learn by the folllowing method:

a) You read something and interpret it.
b) You realize your interpretation has problems/inconsistencies.
c) You ask a bunch of questions on your interpretation.
d) A lot of the questions are like: if this is happening in the lab frame, how can such and such be happening in the rotating frame. Or, if there is no friction in the rotating frame, how come ...

This is illustrated by the fact that if I answer one of your questions it leads to 6 more new questions. So, you didn't really digest my answer. Instead, you thought what else can possibly by wrong with what Morin has said? And the numbers of questions just multiplies. You perhaps need to spend more time analysing your interpretation of what's been said and why it's wrong.

One point: if there is no friction, then nothing moves with the carousel. So, friction on the carousel is what keeps the person going round. Again, you interpreted the statement about friction the wrong way, but instead of analysing your interpretation, you jumped to a wrong conclusion about what Morin meant which generated a lot of questions. You should have said to yourself: that can't be what he means, so what did he mean by no friction?

My suggestion is to analyse the problem from the lab frame first. And only the lab frame. Forget about rotating frames. Analyse the problem in the lab frame; then one question at a time.

Once you understand the problem in the lab frame; analyse the problem in the rotating frame; again, one question at a time.

Try to focus more on why your interpretation is wrong and not why Morin might be wrong. Try to focus on one aspect of the problem at a time.

 

[PeroK]

To give you some help, here is my analysis in the lab frame:

$X$ is at a fixed point a distance $r$ from the centre of a carousel, rotating at angular velocity $\omega$

$X$ has angular momentum of $L = mwr^2$

If $X$ moves towards the centre of the carousel to a point only $r/2$ from the centre (and stops), then the angular momentum has reduced to:

$L = mwr^2/4$

Therefore, by conservation of AM, $X$ cannot move inward using only a radial force. We can calculate the required angular force:

If $X$ moves inward at speed $v$, then:

$\frac{dL}{dt} = 2mwr \frac{dr}{dt} = -2mwr v$

This is the required torque, so an angular force of $F_a = -2mwv$ is needed for X to follow a straight line on the carousal to the centre. $X$ would have to hold onto something or push against the direction of rotation with his feet to stop himself veering off the the right as he moves inward. I like to think of X holding onto a bar at his chest while he staggers inward!

Note that the real force required to maintain this straight line on the carousel is equal and opposite to the fictitious Coriolis force in a rotating reference frame.

That's the problem analysed fully as far as I am concerned. There's nothing more to it than that.

 

[A.T.]

Note that real and fictitious forces come in pairs that are equal and opposite in an accelerating reference frame

Here I would clarify that this has nothing to do with force pairs from Newtons 3rd Law, which doesn't apply to fictitious forces. It just means than if you completely transform away the acceleration that exists in an inertial frame, then the introduced fictitious forces must cancel the real forces, so Newtons 2nd Law is still satisfied.

 

[PeroK]

Here I would clarify that this has nothing to do with force pairs from Newtons 3rd Law, which doesn't apply to fictitious forces. It just means than if you completely transform away the acceleration that exists in an inertial frame, then the introduced fictitious forces must cancel the real forces, so Newtons 2nd Law is still satisfied.

Yes, good point, nothing to do with the 3rd law.

 

[A.T.]

This is the required torque, so an angular force of $F_a = -2mwv$ is needed for X to follow a straight line on the carousal to the centre. $X$ would have to hold onto something or push against the direction of rotation with his feet to stop himself veering off the the right as he moves inward. I like to think of X holding onto a bar at his chest while he staggers inward!

Note that the real force required to maintain this straight line on the carousel is equal and opposite to the fictitious Coriolis force in a rotating reference frame.

That's the problem analysed fully as far as I am concerned. There's nothing more to it than that.

I think the confusing part is about "What if the person doesn’t apply a tangential friction force at his feet?", so the case where there is no torque, but still tangential acceleration in the inertial frame, according to the text.

 

[PeroK]

I think the confusing part is about "What if the person doesn’t apply a tangential friction force at his feet?", so the case where there is no torque, but still tangential acceleration in the inertial frame, according to the text.

Exactly, that's why I thought it was better simply to analyse the problem. There are quite a few posts on PF, where a whole bunch of questions get asked about a problem like this and we end up answering questions about questions about a clarification of something that is in a book.

This thread made me realize how much (ultimately) I rely on my own analysis to understand something and not just someone else's words. I was trying to encourage the OP to do the same, rather than spend a lot of time trying to figure out exactly what Morin is driving at. To tackle the problem independently and identify precisely what you don't understand about the problem.