Calculating Charge on Two Pith Balls Using Coulomb's Law | Homework Help

  • Thread starter Thread starter Hannahj1
  • Start date Start date
  • Tags Tags
    Coulomb's law Law
AI Thread Summary
To calculate the charge on two pith balls using Coulomb's Law, the angle of separation and the masses of the balls are essential. The relevant equation is F = k q Q / d^2, where the net force must consider all acting forces, not just the electric force. A free-body diagram (FBD) is recommended to visualize the forces at play, including tension and gravity. The discussion emphasizes the importance of equilibrium of forces, as the balls remain at rest, indicating no net acceleration. Understanding these concepts is crucial for accurately determining the charge on the pith balls.
Hannahj1
Messages
18
Reaction score
2

Homework Statement


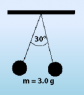
The charge on two pith balls can be calculated by knowing their masses and observing the angle of separation between the balls.
If both balls are equally charged and they are suspended by strings that are 1.0 m long, calculate that charge.

Homework Equations


F = k q Q / d^2

The Attempt at a Solution


fnet=kqQ/d^2
ma=kq^2/d^2 (both q's are the same)
Im a bit stuck here because i don't know how to find the acceleration. Thank you!
 

Attachments

  • Screen Shot 2015-08-18 at 11.06.01 PM.png
    Screen Shot 2015-08-18 at 11.06.01 PM.png
    2.6 KB · Views: 558
Physics news on Phys.org
Hannahj1 said:
Im a bit stuck here because i don't know how to find the acceleration.
The balls remain at rest.
 
Why acceleration?

Why don't you try equilibrium of forces?
 
Have you drawn a free body diagram on either of the balls, or do you feel you have advanced beyond the point where you need to use FBDs?

Chet
 
Hannahj1 said:
fnet=kqQ/d^2

This is not Fnet, because the electric force is not the only one acting on each ball. Your first step should be to choose one ball (either one will work, so you can toss a coin or something), then identify all the forces that act on it and draw a free-body diagram for it as Chet asked for.
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Deriving Pith Ball Mass from Coulomb's Law: A Scientific Exploration
Replies
7
Views
2K
Hanging pith balls on a thread...charge, Fg, Fe and tension
Replies
2
Views
3K
Calculating Charge and Force Using Coulomb's Law and Trigonometry
Replies
6
Views
8K
How to find the mass of a pith ball using electric forces?
Replies
1
Views
3K
Coulomb's law to find electric field for charge density function
Replies
11
Views
1K
How Do You Calculate the Electric Charge on a Suspended Cork Ball?
Replies
2
Views
2K
Charge on pith ball between two plates
Replies
2
Views
3K
What is the minimum charge needed for a ball to jump in an electric field?
Replies
15
Views
1K
Coulomb's Law and 4 point charges
Replies
12
Views
3K
Coulomb's law vs Electric Field
Replies
12
Views
5K

Hot Threads

Recent Insights

Back
Top