Current Carrying Rod On Inclined Plane.

[SherlockOhms]

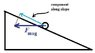
A conductingng bar of mass 1. w kg and length l = 1. x m is placed at rest on a frictionlsss plane inclined at an angle θ = 2 y degrees to the horizontal. A current I= 4 A flows through the bar in the − ˆj direction, and there is a uniform magnetic field B = 1 T in the kˆ direction.
(a)
What is the gravitational force on the bar acting down the plane? (3)
(b)
What is the magnetic force on the bar acting up the plane? (3)
(c)
If the bar is initially at rest, how far does it move along the plane in 0.5 s and specify whether it moves (4) up or down. (Assume zero friction so that the bar slips rather than rolls along the plane. Rolling motion
would be more complicated since rotational kinetic energy would need to be factored into the calculations.)

Ok, so I calculated the gravitational force acting down the plane to be mgSin(theta). That was fine. I then calculated the Magnetic force acting up the plans but it's apparently incorrect.

I crossed L(I) x B and got 4.8(-j) x 1k and got -4.8i as the force in the -I direction, (sort of into the plane). I then said that cos(theta) =h/a, the adjacent in the case being the 4.8i. I found h to be 5. something or other. It's marked as incorrect though. Any ideas?

 

[TSny]

I then said that cos(theta) =h/a, the adjacent in the case being the 4.8i. I found h to be 5. something or other. It's marked as incorrect though. Any ideas?

Is this just a typographical error or did you actually make a mistake in setting up the cosine relation?

 

[SherlockOhms]

Is this just a typographical error or did you actually make a mistake in setting up the cosine relation?

It's just a typo. Apologies for that.

 

[TSny]

I crossed L(I) x B and got 4.8(-j) x 1k and got -4.8i as the force in the -I direction, (sort of into the plane). I then said that cos(theta) =h/a, the adjacent in the case being the 4.8i. I found h to be 5. something or other. It's marked as incorrect though. Any ideas?

Shouldn't the component of the magnetic force along the plane be less than the magnitude of the magnetic force? So, if the magnetic force is 4.8 N, the component along the plane should be less than 4.8 N.

 

[TSny]

I think you might have drawn your little right triangle incorrectly for finding the component of the magnetic force along the plane. The component you are looking for should be the adjacent side of the triangle, not the hypotenuse.

 

[SherlockOhms]

But, the -4.8i just acts into the plane, not parallel to it. The mgsin(theta) which I found is parallel to the plane, acting down it. I thought that the -4.8i was just the i component of the magnetic force. If that isn't the case though, then the magnitude is just |4.8i| and has no j component so therefore there won't be any magnetic force acting on the same plane as the mgsin(theta). Does that make sense?

 

[SherlockOhms]

 

[SherlockOhms]

That's the picture of the slope. See what I mean now?

 

[SherlockOhms]

I think you might have drawn your little right triangle incorrectly for finding the component of the magnetic force along the plane. The component you are looking for should be the adjacent side of the triangle, not the hypotenuse.

If you take a look at the picture you can see that the -4.8i wouldn't actually be the hypotenuse, would it?

 

[TSny]

That's the picture of the slope. See what I mean now?

Yes. IL x B gives the total magnitude of the magnetic force (4.8 N). The 4.8 N acts horizontally in the negative x direction. You need to find the component of that horizontal force along the inclined surface.

 

[SherlockOhms]

So, just 4.8cos(theta)? I was drawing the 4.8 as the side opposite the right angle.

 

[TSny]

So, just 4.8cos(theta)? I was drawing the 4.8 as the side opposite the right angle.

Yes. The 4.8 N is the hypotenuse (which is the side opposite the right angle.) See figure.

 

[SherlockOhms]

Thanks a million man!