Tosh5457
- 130
- 28
I'm translating the problem, so sorry for the errors.
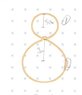
Radius of the upper circumference = 5cm
Radius of the lower circumference = 9cm
Resistance/meter = 3.00 ohm/meter
B is the magnetic field: DB/dt = 2.00 T/s
What's the magnitude of the current, and where does the current points to?
EMF = -N \ \frac{\Delta \Phi_B}{\Delta t} \ \ \mbox{or} \ \ -N \ \frac{d\Phi_B }{dt}
V = RI
Homework Statement
Radius of the upper circumference = 5cm
Radius of the lower circumference = 9cm
Resistance/meter = 3.00 ohm/meter
B is the magnetic field: DB/dt = 2.00 T/s
What's the magnitude of the current, and where does the current points to?
Homework Equations
EMF = -N \ \frac{\Delta \Phi_B}{\Delta t} \ \ \mbox{or} \ \ -N \ \frac{d\Phi_B }{dt}
V = RI
The Attempt at a Solution
Attachments
Last edited: