Curvilinear coordinate system: Determine the standardized base vectors

[Karl Karlsson]

Homework Statement

Determine the standardized base vectors in the curvilinear coordinate system $$\begin{cases} u_1 = x^2-y^2 \\ u_2 = xy \\ u_3 = z\end{cases}$$

Relevant Equations

$$\begin{cases} u_1 = x^2-y^2 \\ u_2 = xy \\ u_3 = z\end{cases}$$

How I would have guessed you were supposed to solve it:

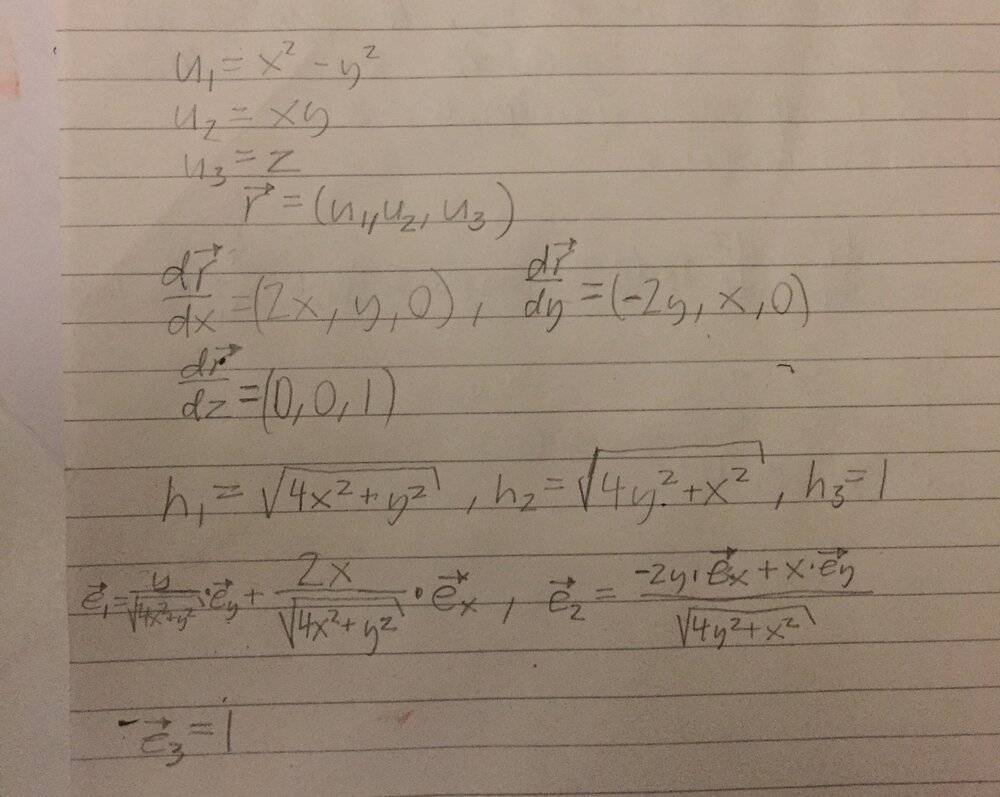
What you are supposed to do is just take the gradients of all the u:s and divide by the absolute value of the gradient? But what formula is that why is the way I did not the correct way to do it?

Thanks in advance!

 

[pasmith]

The position vector is always $\mathbf{r}(u,v,w) = (x(u,v,w),y(u,v,w),z(u,v,w))$. Here you are given $u(x,y,z)$ etc., and you would have to invert this to get $(x,y,z)$ in terms of $(u,v,w)$, but you don't have to.

The basis vector $\mathbf{e}_{u_i}$ points in the direction of increasing $u_i$ and is normal to surfaces of constant $u_i$. The vector $\nabla u_i$ does exactly this.

Now it turns out that if the $\nabla u_i$ are orthogonal then $\nabla u_i$ and $\frac{\partial \mathbf{r}}{\partial u_i}$ are parallel.

 

[Karl Karlsson]

The position vector is always $\mathbf{r}(u,v,w) = (x(u,v,w),y(u,v,w),z(u,v,w))$. Here you are given $u(x,y,z)$ etc., and you would have to invert this to get $(x,y,z)$ in terms of $(u,v,w)$, but you don't have to.

The basis vector $\mathbf{e}_{u_i}$ points in the direction of increasing $u_i$ and is normal to surfaces of constant $u_i$. The vector $\nabla u_i$ does exactly this.

Now it turns out that if the $\nabla u_i$ are orthogonal then $\nabla u_i$ and $\frac{\partial \mathbf{r}}{\partial u_i}$ are parallel.

Is it because they have taken $grad φ = \sum_{i} \frac {1} {h_i} \frac {\partial φ} {\partial u_i}$ and $φ=u_i$?