- #1
I_am_learning
- 682
- 16
the solution for current I, for series LCR circuit is
I = (E/Z)sin(wt+[tex]\phi[/tex])
Where Z = [tex]\sqrt{R^2 + (X_{L}-X_{C})^{2}}[/tex]
So for Resonance (i.e. maximum Current Amplitude) of LCR Circuit the necessary condition seems to be
[tex]X_{L}[/tex]=[tex]X_{C}[/tex]
Which gives [tex]\omega[/tex]=1/[tex]\sqrt{LC}[/tex]
But some text-books and wikipaedia have given that the damped resonace frequency is
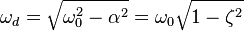
where
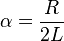
How is this relation Derived ?
I = (E/Z)sin(wt+[tex]\phi[/tex])
Where Z = [tex]\sqrt{R^2 + (X_{L}-X_{C})^{2}}[/tex]
So for Resonance (i.e. maximum Current Amplitude) of LCR Circuit the necessary condition seems to be
[tex]X_{L}[/tex]=[tex]X_{C}[/tex]
Which gives [tex]\omega[/tex]=1/[tex]\sqrt{LC}[/tex]
But some text-books and wikipaedia have given that the damped resonace frequency is
where
How is this relation Derived ?
Last edited: