DC Motor Question: Change in Magnetic Flux

[gaobo9109]

Homework Statement

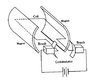
A simple DC motor consists of an armature placed between two poles of a magnet. The armature is rectangular and has dimensions of 90mm in breadth and 100mm in length. Magnetic flux density produced by the magnet is 0.5T. Number of turns of armature winding is 500. What is the change in magnetic flux when the armature is rotated through 360 degree

Homework Equations

The Attempt at a Solution

The answer I have arrived at is different from the answer provided.

My answer is as follow:

Change in magnetic flux = Area of the armature x magnetic flux density x 2
= 90mm x 100mm x 0.5T x 2

The answer provided is:

Change in magnetic flux = B x [Area swept in one revolution by each 100mm-side] x [2 sides]
= 0.5T x 2pi(90mm/2)(100mm) x 2

I have no idea how that answer is arrived at.

 

[Simon Bridge]

What was the rationale for yours?

The armature is rotating - the 100mm sides move in a circle, so the area swept out by each one is the surface of a cylinder.

 

[gneill]

The so-called solution seems a bit odd to me. Why would the area swept out by a side matter?

Usually the flux referred to in these rotating coil problems is the flux that passes through the cross-sectional area that is defined by the plane of the coil. Since the coil rotates in the field, it will vary from some maximum value, to zero, and back again to the maximum value through a 360° rotation. The maximum value occurs when the plane of the coil is perpendicular to the magnetic field (so that the presented cross sectional area of the coil is maximum).

 

[Simon Bridge]

Did they provide a diagram of the setup? Perhaps the magnetic field has a cylindrical symmetry?

Like this one:
http://media.wiley.com/product_data/excerpt/9X/04716844/047168449X.pdf
... Each example is treated two ways.

 

[gaobo9109]

The diagram provided in the question is quite similar to the one I have attached, except that the coil is substituted with a rectangular armature with wire around it.

I find the solution weird because normally I would calculate change in magnetic flux by finding change in the magnetic field perpendicular to the coil and multiply it to the area of the coil. However, solution considers surface area swept by the coil, which I have never seen before.

You said that there are two ways to calculate change in magnetic flux. What is the rationale for the second approach and when do you use the second approach?

 

[Simon Bridge]

iirc - you can use Faraday's Law or Gausses Law. Gausses Law has integral and differential forms. They are actually forms of the same thing - you use the one that makes the math easiest.

Did you read the reference provided? - it shows how you use Faraday's Law for a motor with a cylindrically symmetric B field - it's radial in the vicinity of the wire. It would be better if there was an iron core inside the loop though. Even so, the flux-density half-way between the magnets is still higher than that by the poles.

It's a bit mean because you are used to rectangular fields.