deimors
- 13
- 0
Hi,
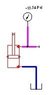
I've been trying to figure out a formula which describes the relation between the area, load and negative psig of the vacuum created in a vertical cylinder with the top port plugged and the bottom draining to tank (fig 1). I searched around for a formula describing this, and upon having no luck, decided to dive in and figure it out myself, using data I gathered from simulation software to find a decent formula.
After mucking about for a bit, I was able to come up with the equation:
P(L, A) = ((((L / (46 * A)) + 1.1)^-2) - 1) * 14.04
where P = pressure (psig), A = area (in^2) and L = load (lbs)
Now, I recognize that a complete vacuum is -14.7 psig (0 psia), but setting the horizontal asymptote at -14.04 seems to fit the curve to the data best.
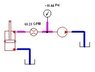
This seems all well and good to me, and so now I'm trying to deduce the pressure in situations where flow is moving in or out of the top port (as in fig 2). After some more messing about with spreadsheets, I came up with the following equation:
P(L, A, Q) = ((((L / (46 * A)) - (Q / 82.2) + 1.1)^-2) - 1) * 14.04
where Q is flow, such that positive values of Q represent flow directed into the cylinder
This seems pretty cool until I play around with it a bit and realize that there's a vertical asymptote at Q = ((L / (46 * A)) + 1.1) * 82.2.
So I suppose my question would be: is there a formula out there describing this relation that I should be using instead, or barring that (and I can't imagine this formula isn't out there _somewhere_), is there a way I could deal with this problematic asymptote?
Any help on this matter would be greatly appreciated.
I've been trying to figure out a formula which describes the relation between the area, load and negative psig of the vacuum created in a vertical cylinder with the top port plugged and the bottom draining to tank (fig 1). I searched around for a formula describing this, and upon having no luck, decided to dive in and figure it out myself, using data I gathered from simulation software to find a decent formula.
After mucking about for a bit, I was able to come up with the equation:
P(L, A) = ((((L / (46 * A)) + 1.1)^-2) - 1) * 14.04
where P = pressure (psig), A = area (in^2) and L = load (lbs)
Now, I recognize that a complete vacuum is -14.7 psig (0 psia), but setting the horizontal asymptote at -14.04 seems to fit the curve to the data best.
This seems all well and good to me, and so now I'm trying to deduce the pressure in situations where flow is moving in or out of the top port (as in fig 2). After some more messing about with spreadsheets, I came up with the following equation:
P(L, A, Q) = ((((L / (46 * A)) - (Q / 82.2) + 1.1)^-2) - 1) * 14.04
where Q is flow, such that positive values of Q represent flow directed into the cylinder
This seems pretty cool until I play around with it a bit and realize that there's a vertical asymptote at Q = ((L / (46 * A)) + 1.1) * 82.2.
So I suppose my question would be: is there a formula out there describing this relation that I should be using instead, or barring that (and I can't imagine this formula isn't out there _somewhere_), is there a way I could deal with this problematic asymptote?
Any help on this matter would be greatly appreciated.