Decomposing velocity vectors into polar axis

[Like Tony Stark]

Homework Statement

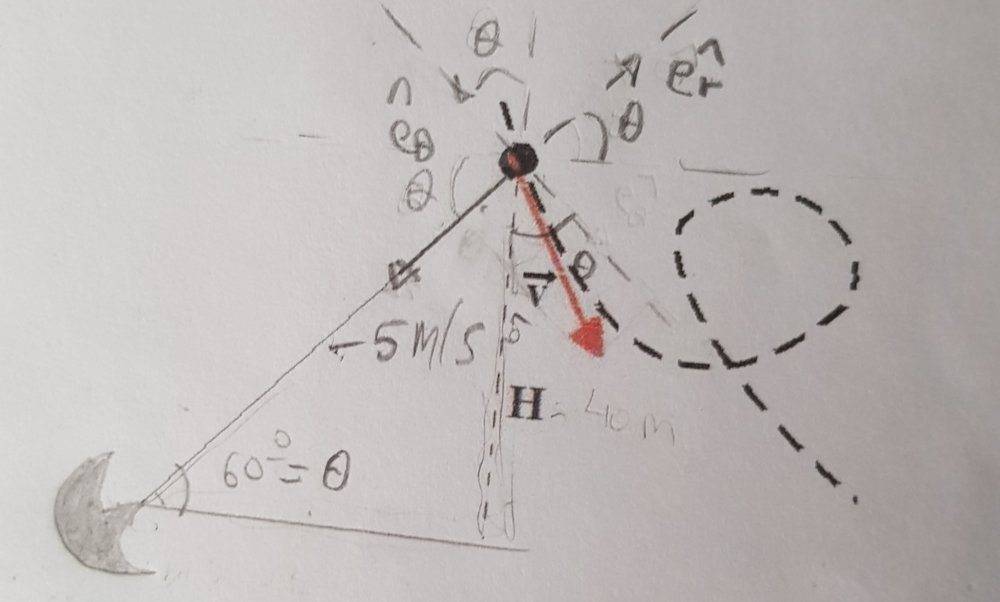
A particle moves along a trajectory with velocity whose modulus is constant. At a certain time it is at a point of the trajectory whose radius of curvature is 15 m. At this moment, the modulus of the acceleration is 10 m/s^2. A radar detects that the particle, located 40 m above the ground, moves towards it with velocity v=5 m/s. The radius vector that goes from the radar to the particle forms an angle of 60° with the ground.
Find the angle formed by the velocity and the angular coordinate.

Relevant Equations

v=(dot r; r dot theta) in polar coordinates

Well, I drew the polar and standard axis centered in the particle and wrote which angles were equal to 60° so I could decompose the velocity. The problem says "moves towards it (the radar) with velocity v=5 m/s, so that's one of the components. But I realized that the velocity "cuts" the angle, so I don't know how I should decompose the velocity. Maybe it's a silly question, but it confuses me.

 

[tnich]

The angular component is perpendicular to the radial component, so draw it at a right angle from the head of the radial component toward the velocity vector.

 

[Like Tony Stark]

The angular component is perpendicular to the radial component, so draw it at a right angle from the head of the radial component toward the velocity vector.

So the velocity would have the same direction that the angular component?

 

[tnich]

No, that would just be the way to draw than angular component. The angular velocity component is perpendicular to the radial component (radial with respect to the radar's positions). Their vector sum is the velocity vector.

 

[tnich]

No, that would just be the way to draw than angular component. The angular velocity component is perpendicular to the radial component (radial with respect to the radar's positions). Their vector sum is the velocity vector.

It looks like you are stuck on this part. You need to decompose the velocity vector into two perpendicular components, one pointing toward the radar. Maybe a picture would help.